1. Syntax
{
"cells": [
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Task\n",
"The second assignment deals with Random Forests. Random forests are predictive models that allow for a data driven exploration of many explanatory variables in predicting a response or target variable. Random forests provide importance scores for each explanatory variable and also allow you to evaluate any increases in correct classification with the growing of smaller and larger number of trees.\n",
"\n",
"Run a Random Forest.\n",
"\n",
"You will need to perform a random forest analysis to evaluate the importance of a series of explanatory variables in predicting a binary, categorical response variable."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Data\n",
"The dataset is related to red variants of the Portuguese \"Vinho Verde\" wine. Due to privacy and logistic issues, only physicochemical (inputs) and sensory (the output) variables are available (e.g. there is no data about grape types, wine brand, wine selling price, etc.). \n",
"\n",
"The classes are ordered and not balanced (e.g. there are munch more normal wines than excellent or poor ones). Outlier detection algorithms could be used to detect the few excellent or poor wines. Also, we are not sure if all input variables are relevant. So it could be interesting to test feature selection methods. \n",
"\n",
"Dataset can be found at [UCI Machine Learning Repository](http://archive.ics.uci.edu/ml/datasets/Wine+Quality)\n",
"\n",
"Attribute Information (For more information, read [Cortez et al., 2009]): \n",
"Input variables (based on physicochemical tests): \n",
"* 1 - fixed acidity \n",
"* 2 - volatile acidity \n",
"* 3 - citric acid \n",
"* 4 - residual sugar \n",
"* 5 - chlorides \n",
"* 6 - free sulfur dioxide \n",
"* 7 - total sulfur dioxide \n",
"* 8 - density \n",
"* 9 - pH \n",
"* 10 - sulphates \n",
"* 11 - alcohol \n",
"\n",
"Output variable (based on sensory data): \n",
"* 12 - quality (score between 0 and 10)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Results"
]
},
{
"cell_type": "markdown",
"metadata": {
"collapsed": true
},
"source": [
"Random forest and ExtraTrees classifier were deployed to evaluate the importance of a series of explanatory variables in predicting a categorical response variable - red wine quality (score between 0 and 10). The following explanatory variables were included: fixed acidity, volatile acidity, citric acid, residual sugar, chlorides, free sulfur dioxide, total sulfur dioxide, density, pH, sulphates and alcohol.\n",
"\n",
"The explanatory variables with the highest importance score (evaluated by both classifiers) are alcohol, volatile acidity, sulphates. The accuracy of the Random forest and ExtraTrees clasifier is about 67%, which is quite good for highly unbalanced and hardly distinguished from each other classes. The subsequent growing of multiple trees rather than a single tree, adding a lot to the overall score of the model. For Random forest the number of estimators is 20, while for ExtraTrees classifier - 12, because the second classifier grows up much faster."
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"### Code"
]
},
{
"cell_type": "code",
"execution_count": 1,
"metadata": {},
"outputs": [],
"source": [
"import pandas as pd\n",
"import numpy as np\n",
"import matplotlib.pylab as plt\n",
"from sklearn.model_selection import train_test_split, cross_val_score\n",
"from sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifier\n",
"from sklearn.manifold import MDS\n",
"from sklearn.metrics.pairwise import pairwise_distances\n",
"from sklearn.metrics import accuracy_score\n",
"import seaborn as sns\n",
"%matplotlib inline\n",
"\n",
"rnd_state = 4536"
]
},
{
"cell_type": "code",
"execution_count": 2,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"<class 'pandas.core.frame.DataFrame'>\n",
"RangeIndex: 1599 entries, 0 to 1598\n",
"Data columns (total 12 columns):\n",
"fixed acidity 1599 non-null float64\n",
"volatile acidity 1599 non-null float64\n",
"citric acid 1599 non-null float64\n",
"residual sugar 1599 non-null float64\n",
"chlorides 1599 non-null float64\n",
"free sulfur dioxide 1599 non-null float64\n",
"total sulfur dioxide 1599 non-null float64\n",
"density 1599 non-null float64\n",
"pH 1599 non-null float64\n",
"sulphates 1599 non-null float64\n",
"alcohol 1599 non-null float64\n",
"quality 1599 non-null int64\n",
"dtypes: float64(11), int64(1)\n",
"memory usage: 150.0 KB\n"
]
}
],
"source": [
"data = pd.read_csv('Data\\winequality-red.csv', sep=';')\n",
"data.info()"
]
},
{
"cell_type": "code",
"execution_count": 3,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>fixed acidity</th>\n",
" <th>volatile acidity</th>\n",
" <th>citric acid</th>\n",
" <th>residual sugar</th>\n",
" <th>chlorides</th>\n",
" <th>free sulfur dioxide</th>\n",
" <th>total sulfur dioxide</th>\n",
" <th>density</th>\n",
" <th>pH</th>\n",
" <th>sulphates</th>\n",
" <th>alcohol</th>\n",
" <th>quality</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>0</th>\n",
" <td>7.4</td>\n",
" <td>0.70</td>\n",
" <td>0.00</td>\n",
" <td>1.9</td>\n",
" <td>0.076</td>\n",
" <td>11.0</td>\n",
" <td>34.0</td>\n",
" <td>0.9978</td>\n",
" <td>3.51</td>\n",
" <td>0.56</td>\n",
" <td>9.4</td>\n",
" <td>5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>1</th>\n",
" <td>7.8</td>\n",
" <td>0.88</td>\n",
" <td>0.00</td>\n",
" <td>2.6</td>\n",
" <td>0.098</td>\n",
" <td>25.0</td>\n",
" <td>67.0</td>\n",
" <td>0.9968</td>\n",
" <td>3.20</td>\n",
" <td>0.68</td>\n",
" <td>9.8</td>\n",
" <td>5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>2</th>\n",
" <td>7.8</td>\n",
" <td>0.76</td>\n",
" <td>0.04</td>\n",
" <td>2.3</td>\n",
" <td>0.092</td>\n",
" <td>15.0</td>\n",
" <td>54.0</td>\n",
" <td>0.9970</td>\n",
" <td>3.26</td>\n",
" <td>0.65</td>\n",
" <td>9.8</td>\n",
" <td>5</td>\n",
" </tr>\n",
" <tr>\n",
" <th>3</th>\n",
" <td>11.2</td>\n",
" <td>0.28</td>\n",
" <td>0.56</td>\n",
" <td>1.9</td>\n",
" <td>0.075</td>\n",
" <td>17.0</td>\n",
" <td>60.0</td>\n",
" <td>0.9980</td>\n",
" <td>3.16</td>\n",
" <td>0.58</td>\n",
" <td>9.8</td>\n",
" <td>6</td>\n",
" </tr>\n",
" <tr>\n",
" <th>4</th>\n",
" <td>7.4</td>\n",
" <td>0.70</td>\n",
" <td>0.00</td>\n",
" <td>1.9</td>\n",
" <td>0.076</td>\n",
" <td>11.0</td>\n",
" <td>34.0</td>\n",
" <td>0.9978</td>\n",
" <td>3.51</td>\n",
" <td>0.56</td>\n",
" <td>9.4</td>\n",
" <td>5</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" fixed acidity volatile acidity citric acid residual sugar chlorides \\\n",
"0 7.4 0.70 0.00 1.9 0.076 \n",
"1 7.8 0.88 0.00 2.6 0.098 \n",
"2 7.8 0.76 0.04 2.3 0.092 \n",
"3 11.2 0.28 0.56 1.9 0.075 \n",
"4 7.4 0.70 0.00 1.9 0.076 \n",
"\n",
" free sulfur dioxide total sulfur dioxide density pH sulphates \\\n",
"0 11.0 34.0 0.9978 3.51 0.56 \n",
"1 25.0 67.0 0.9968 3.20 0.68 \n",
"2 15.0 54.0 0.9970 3.26 0.65 \n",
"3 17.0 60.0 0.9980 3.16 0.58 \n",
"4 11.0 34.0 0.9978 3.51 0.56 \n",
"\n",
" alcohol quality \n",
"0 9.4 5 \n",
"1 9.8 5 \n",
"2 9.8 5 \n",
"3 9.8 6 \n",
"4 9.4 5 "
]
},
"execution_count": 3,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data.head()"
]
},
{
"cell_type": "code",
"execution_count": 4,
"metadata": {},
"outputs": [
{
"data": {
"text/html": [
"<div>\n",
"<style>\n",
" .dataframe thead tr:only-child th {\n",
" text-align: right;\n",
" }\n",
"\n",
" .dataframe thead th {\n",
" text-align: left;\n",
" }\n",
"\n",
" .dataframe tbody tr th {\n",
" vertical-align: top;\n",
" }\n",
"</style>\n",
"<table border=\"1\" class=\"dataframe\">\n",
" <thead>\n",
" <tr style=\"text-align: right;\">\n",
" <th></th>\n",
" <th>fixed acidity</th>\n",
" <th>volatile acidity</th>\n",
" <th>citric acid</th>\n",
" <th>residual sugar</th>\n",
" <th>chlorides</th>\n",
" <th>free sulfur dioxide</th>\n",
" <th>total sulfur dioxide</th>\n",
" <th>density</th>\n",
" <th>pH</th>\n",
" <th>sulphates</th>\n",
" <th>alcohol</th>\n",
" <th>quality</th>\n",
" </tr>\n",
" </thead>\n",
" <tbody>\n",
" <tr>\n",
" <th>count</th>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" <td>1599.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>mean</th>\n",
" <td>8.319637</td>\n",
" <td>0.527821</td>\n",
" <td>0.270976</td>\n",
" <td>2.538806</td>\n",
" <td>0.087467</td>\n",
" <td>15.874922</td>\n",
" <td>46.467792</td>\n",
" <td>0.996747</td>\n",
" <td>3.311113</td>\n",
" <td>0.658149</td>\n",
" <td>10.422983</td>\n",
" <td>5.636023</td>\n",
" </tr>\n",
" <tr>\n",
" <th>std</th>\n",
" <td>1.741096</td>\n",
" <td>0.179060</td>\n",
" <td>0.194801</td>\n",
" <td>1.409928</td>\n",
" <td>0.047065</td>\n",
" <td>10.460157</td>\n",
" <td>32.895324</td>\n",
" <td>0.001887</td>\n",
" <td>0.154386</td>\n",
" <td>0.169507</td>\n",
" <td>1.065668</td>\n",
" <td>0.807569</td>\n",
" </tr>\n",
" <tr>\n",
" <th>min</th>\n",
" <td>4.600000</td>\n",
" <td>0.120000</td>\n",
" <td>0.000000</td>\n",
" <td>0.900000</td>\n",
" <td>0.012000</td>\n",
" <td>1.000000</td>\n",
" <td>6.000000</td>\n",
" <td>0.990070</td>\n",
" <td>2.740000</td>\n",
" <td>0.330000</td>\n",
" <td>8.400000</td>\n",
" <td>3.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>25%</th>\n",
" <td>7.100000</td>\n",
" <td>0.390000</td>\n",
" <td>0.090000</td>\n",
" <td>1.900000</td>\n",
" <td>0.070000</td>\n",
" <td>7.000000</td>\n",
" <td>22.000000</td>\n",
" <td>0.995600</td>\n",
" <td>3.210000</td>\n",
" <td>0.550000</td>\n",
" <td>9.500000</td>\n",
" <td>5.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>50%</th>\n",
" <td>7.900000</td>\n",
" <td>0.520000</td>\n",
" <td>0.260000</td>\n",
" <td>2.200000</td>\n",
" <td>0.079000</td>\n",
" <td>14.000000</td>\n",
" <td>38.000000</td>\n",
" <td>0.996750</td>\n",
" <td>3.310000</td>\n",
" <td>0.620000</td>\n",
" <td>10.200000</td>\n",
" <td>6.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>75%</th>\n",
" <td>9.200000</td>\n",
" <td>0.640000</td>\n",
" <td>0.420000</td>\n",
" <td>2.600000</td>\n",
" <td>0.090000</td>\n",
" <td>21.000000</td>\n",
" <td>62.000000</td>\n",
" <td>0.997835</td>\n",
" <td>3.400000</td>\n",
" <td>0.730000</td>\n",
" <td>11.100000</td>\n",
" <td>6.000000</td>\n",
" </tr>\n",
" <tr>\n",
" <th>max</th>\n",
" <td>15.900000</td>\n",
" <td>1.580000</td>\n",
" <td>1.000000</td>\n",
" <td>15.500000</td>\n",
" <td>0.611000</td>\n",
" <td>72.000000</td>\n",
" <td>289.000000</td>\n",
" <td>1.003690</td>\n",
" <td>4.010000</td>\n",
" <td>2.000000</td>\n",
" <td>14.900000</td>\n",
" <td>8.000000</td>\n",
" </tr>\n",
" </tbody>\n",
"</table>\n",
"</div>"
],
"text/plain": [
" fixed acidity volatile acidity citric acid residual sugar \\\n",
"count 1599.000000 1599.000000 1599.000000 1599.000000 \n",
"mean 8.319637 0.527821 0.270976 2.538806 \n",
"std 1.741096 0.179060 0.194801 1.409928 \n",
"min 4.600000 0.120000 0.000000 0.900000 \n",
"25% 7.100000 0.390000 0.090000 1.900000 \n",
"50% 7.900000 0.520000 0.260000 2.200000 \n",
"75% 9.200000 0.640000 0.420000 2.600000 \n",
"max 15.900000 1.580000 1.000000 15.500000 \n",
"\n",
" chlorides free sulfur dioxide total sulfur dioxide density \\\n",
"count 1599.000000 1599.000000 1599.000000 1599.000000 \n",
"mean 0.087467 15.874922 46.467792 0.996747 \n",
"std 0.047065 10.460157 32.895324 0.001887 \n",
"min 0.012000 1.000000 6.000000 0.990070 \n",
"25% 0.070000 7.000000 22.000000 0.995600 \n",
"50% 0.079000 14.000000 38.000000 0.996750 \n",
"75% 0.090000 21.000000 62.000000 0.997835 \n",
"max 0.611000 72.000000 289.000000 1.003690 \n",
"\n",
" pH sulphates alcohol quality \n",
"count 1599.000000 1599.000000 1599.000000 1599.000000 \n",
"mean 3.311113 0.658149 10.422983 5.636023 \n",
"std 0.154386 0.169507 1.065668 0.807569 \n",
"min 2.740000 0.330000 8.400000 3.000000 \n",
"25% 3.210000 0.550000 9.500000 5.000000 \n",
"50% 3.310000 0.620000 10.200000 6.000000 \n",
"75% 3.400000 0.730000 11.100000 6.000000 \n",
"max 4.010000 2.000000 14.900000 8.000000 "
]
},
"execution_count": 4,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"data.describe()"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### Plots\n",
"For visualization purposes, the number of dimensions was reduced to two by applying MDS method with cosine distance. The plot illustrates that our classes are not clearly divided into parts."
]
},
{
"cell_type": "code",
"execution_count": 5,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Wall time: 38.7 s\n"
]
}
],
"source": [
"model = MDS(random_state=rnd_state, n_components=2, dissimilarity='precomputed')\n",
"%time representation = model.fit_transform(pairwise_distances(data.iloc[:, :11], metric='cosine'))"
]
},
{
"cell_type": "code",
"execution_count": 6,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAs4AAAEKCAYAAAACfdMTAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzs3Xd8XNWd9/HPuWWKRr03q1iWe8MVF6qBQCAxkAYk1NRN\nI0/YfbbkYVM2yZJks9n0hM0mkLJJgNADmGCwce9dtmwVy+q9T7vlPH/MWMUaGwMGO+G8efll6c6d\ne8/MaMx3jn73d4SUEkVRFEVRFEVRzkw73wNQFEVRFEVRlL8GKjgriqIoiqIoyllQwVlRFEVRFEVR\nzoIKzoqiKIqiKIpyFlRwVhRFURRFUZSzoIKzoiiKoiiKopwFFZwVRVEURVEU5Syo4KwoiqIoiqIo\nZ0EFZ0VRFEVRFEU5C8b5HsCZZGdny7KysvM9DEVRlNdt165dXVLKnPM9jreT+jdbUZS/Vmf7b/YF\nHZzLysrYuXPn+R6GoijK6yaEaDjfYzhJCDEN+OOYTZOBfwV+Hd9eBhwHPiil7I3f55+BjwIO8Hkp\n5ZrXOo/6N1tRlL9WZ/tvtirVUBRF+RsnpayWUs6XUs4HFgJB4Angn4C1UspKYG38e4QQM4FbgFnA\ntcBPhBD6eRm8oijKBUQFZ0VRlHeWVUCtlLIBWA08HN/+MHBj/OvVwB+klBEpZT1QAyx520eqKIpy\ngVHBWVEU5Z3lFuD38a/zpJSt8a/bgLz410VA45j7NMW3KYqivKOp4KwoivIOIYTwAO8FHj31Niml\nBOQbOOYnhBA7hRA7Ozs7z8EoFUVRLlwqOCuKorxzXAfsllK2x79vF0IUAMT/7ohvbwYmjblfcXzb\nBFLKB6WUi6SUi3Jy3lFNRBRFeQdSwVlRFOWd41ZGyzQAngbujH99J/DUmO23CCG8QohyoBLY/raN\nUlEU5QJ1QbejUxRFUc4NIUQAuBr45JjNDwCPCCE+CjQAHwSQUh4SQjwCVAE28BkppfM2D1lRFOWC\no4KzoijKO4CUchjIOmVbN7EuG4n2/wbwjbdhaIqiKH81VKmGoiiKoiiKopwFNeOsKIqiKO8gP/vt\n7873EF7Tpz7y4fM9BEVJSAVnRTnPekMOe1pDJHs0FhT6MTRxvoekKIqiKEoCKjgryutwLNTCloGj\npOh+VqXPJdXwv6nj/Wp3Nw/u6kEKFwEETJ2f3TCJKVneczNgRVEURVHOGRWcFeUsSCn5asMjPN+z\nGwcXQ+h8u/EJfjjlYyxKmfKGjrm9eYif7erCdXVAB6DfkXz82eOsvWMqmlAzz4qiKIpyIVHBWVHO\nwvr+Q7zQu4ewtACw4p25vlD7K16Z9zVMoZ/2voPDw2zbt5/Gtja8HpN506czs6KCn+1rjIfmsQRD\nUYetLf0sL0p/qx6OoiiKoihvgArOinIWnuzaTsiNTtjuSpc9Q3UsSakc2RaNWOx55SjDfWGKZmax\n8egu7FCQsppDlBw/itR09q9cRVPqAiBz4skE7BtoUcFZURRFUS4wKjgryllwcE9zi8CVkiEnzMt9\nBzje3EbooRCZXckgofbZdtwCneWdT5HR143h2ADYz/yR3FtNerTlCNccf0ipMS1XlWkoiqIoyoXm\nnPRxFkJcK4SoFkLUCCH+KcHt04UQW4QQESHE35+LcyrK2+mGzEX4Nc+E7RJJY0s7V+y5n68ff5SH\nQut55IPbeeXyw+CAcAVam4ca30r2mDeyyX87teYScAQf3vwswt+D1Kz4sVykZmGUbOeSzDdWN60o\niqIoylvnTc84CyF04MfElnJtAnYIIZ6WUlaN2a0H+Dxw45s9n6KcD1dnzGVN7142Dxwh7EYxhYFA\nULbJz9fnPw7++Axx/B1VPaON8rocyutyEI6gU1agmbEb+80UNl2ZC9lZvF87ytH0IFXBchzDxcg7\nys/mv++MNdOKoiiKopwf56JUYwlQI6WsAxBC/AFYDYwEZyllB9AhhLj+HJxPUd5ywUiY/9j2J9YN\nHiJJerirdBXfnX0ne4bq2TRwhFQjic61LTx6bD36RX4cxpdW2B6HqtnNlNflxDa4ghSnHa8McuBG\nh1RRhOnq4MK8QZMpZhuLL1vIpRnX4tFUBZWiKIqiXIjORalGEdA45vum+LY3RAjxCSHETiHEzs7O\nzjc9OEV5vYKRMKvW3c+fzJ1054dpzOvn34Ye54sv/ZwFKZP5XNG7KQst5rE/baLICeJFJjyOrQks\nTSA1SXdpM8WBx9hXeoBUkYEpR2eUDamTZHno2VOlQrOiKIqiXMAuuP9LSykfBB4EWLRoUeJEoihv\noe9uf5xgqg2e+CyyJsADL6dU09jbycEuL998tRNpW9zR1MED4pTOGLYXs/5y2vvK+dVKQUYoTM+c\nfTxx1VSm7UpjcYKfalPqNDSfQEqJUP2bFUVRFOWCdC5mnJuBSWO+L45vU5S/SusHDo2G5rEceOLI\nJn6wtZuwLckuKmSSbfHZp9swLYlpueBKPNXvQfSXIYWGFILuJB+yfjWW7SWYZuMmOLQlHAZDGTz5\nX1to7e3hSG0/e9c301HTh5Tq86OiKIqiXAjOxYzzDqBSCFFOLDDfAtx2Do6rKOdFEh5wg7GZ5rEE\nJHsC9IZii59kzlnGvxcspCWrAt/+AaLZdczoaabBTsMec3Gf9HfhlK5H+iLUTY2wrN7BcDS0MXXR\nErh+2zMMiuPs+MeNbC32k9NQhj/qISPPz3vuX0pSmlqGW1EUZawDd9x8vofwmub8+vHzPQTlHHrT\nM85SShv4LLAGOAw8IqU8JIT4lBDiUwBCiHwhRBPwReD/CSGahBCpb/bcivJWuGfy1WCfstGVaBbc\nNvdy/GbsbXNUK6cxZyqW7iEis5GdS2iI3oAY0/JZegawpz+JTO4AAa4OT006TI83iC3c2EyzHqG/\no4kNOct5smwOVZmCj+16nLLkTRiOS3/rMK/8aN/b9wQoiqIoipLQOalxllI+Bzx3yrafjfm6jVgJ\nh6Jc8G6csZxNa6t4URwCBxCgWfAfhXfgM01un5fOL3f3ELFBl5JrGl7lqsYthHUPT1asYnfurJFj\nOXn7QIxP4QPeKH8qqyIQNNBbfRhtN2C4FzFU6sMVgl1yAWsKruPLu75OQ8F0/G35tB3uJjwUxZc8\nsZe0oiiKoihvjwvu4kDlb4sjXXRxTtbZOeeGukLUb29DOpLSRXmkFQRGbvvOqo/xhf4unqzeTIY3\nmffPuhSPEXu73HVRBk3dg/z5yADf3fyflA41YBBbxGROz2GeLr+CX85+P0KayKRO0CQ4Ogzlgb8X\nBBDMYjjQASWDVJwI0xxIx9Viz5MLDGsa35t7L/924D/p0lLptebwzGf6KLxsDos+NA1vwDz14SiK\noiiK8hZTwVl5S6zp2cv3mp+hNdpLhhHg4wVXc1vOJRdMx4gjrzSy5aEqpASkZNdjx5i/uoKLbh5d\nsS/bn8qUYA5tDT3s5xgL507H7eli6He/JH/zPq4uvmZcaAYwsFhdv5YGcxFby0oZHM7C8beBlQIp\n7aDF6qNJaYFIClM6IrT680ZC80lSE7QGsjEjQWYOtxHR6gkGM9myLoPWAx1cVbodq/oAVlYuXP8+\n8pcuR9MSf0Cxm09gN53AKC7BKCoBIBSOUN/chOu6lBYWkhIIJLyvoiiKoiijVHBWzrl1fYf41+O/\nJyxjgbLXHuYHzc9huy535l9+fgcHBHvDbHmoCscaU4zsSPY+XUvpojwyS1I40dzGx/7+60SiFpFo\nFI9pMrkojy+1bicQCTHkpnNp/ZZxofmkiNBpLu4lGMhFa1sEwTycwh2joRlAc8EcZt5Rk5bU03TN\nENAdMMgYBq9r4aEdzQox0BZhZ2MEjywhrbWVzIP/ynOXXsuCj9xFYW7uyN1lNELfA/cT2bcbYRhI\n28Yz9yJ6bv8Ua3fsGrk0cdPu3SydO5f5M2acg2dXURRFUf52XZi/Q1f+qv2w+c8jofmksBvlv9v+\ngivd09zr7dOwu4NEE9+u7VK3rRWAf/nyd+jrHyQYCuM4LqFwhCO1DTwZ8qAhmS1C2I7ATfAW+tz1\nn+ZI4CKw0hB2AK2nEvPIzWDH65MlzOrN5c76OWROms+HUvYy3WgbdwzhSnKG+3ny4pRx2xeEHkeX\nFg3mAo56LmG3/0a2eG9n2tYN/PmVdUSt0ed98OGfE9m3C6IRZHAYohEGjxxi7ZZtOI6DHf/jOC7b\n9h+gu6/vTT6ziqIoivK3TQVn5ZxrjvYk3B5yIwTd6Ns8mgTO1BZZQuvaF6lr6Zywm4NgnYwF2TmE\nOSh9E4Lz4Zx82sUshBytQRbo4HjQumYCMKMvm6WdxfhcA00IPLpksa+J6Vo7AIbj4HEcFkb/l0W1\nA/x65RT+d/4yDictJcntZ0Xw14AGQuAIL0NaFo3uRXgiIWpPjC7iGXrxWYiOf77bcgrBPrVlCLiu\ny7Hjx8/8vAENdW38030/4aYP/F8+/clvs2f70dhxO7ppam1XPacVRVGUv2mqVEM550q9ORwJTVwD\nJ6D5SNJGu0LsHqzjZ61raAh3MjNQzN8VXMvUpMK3fHwlC3PZ+pvDE7Zrhkb5xfl0fe3LxN4aE6el\nT8ZCIeAWZy/7PJcwz9qERGAQZUfRFIRwQI5/awlpIgYKIX8vC7uLxi25DWAIyWLPcWgZxLC7GDz2\nCutu9vJ83hQsHQxb8sdrdD7wh1tZ3rqJ48OPUycmMcc7lWwjgxZjFhHdJjImKMtoZML4XU1L9LCQ\nUuK4Zw69Rw4c56P/9HVs6eDi0jzcwe6vHCYrI53+4UEQgsz0VL75j59m9vSKMx5LefsJIdKBXwCz\nif0o3wNUA38EyoDjwAellL3x/f8Z+Cix3jKfl1KueftHrSiKcmFRM87KOXdv8Q34xPiuDz7N5DNF\n16HFO2ys6zvE39X8nG2Dx2iz+nil7xC3V3+fg8MnRu7T1zzEyz/Yw+8/+wrPfHUrTfs6z8n4Ahk+\nlt0xA93U0AwNoQN5DsXvzsCfY5LW0UwhNhOnpiWXMDzynUc4zLE2UmdOY1dSAVEEk3s7SBy4HfAM\ngqOR5CTuiGEYgkvTa2jP7aT2PfkM5vuIekDqYHkdwj6L595zmCPea0hzBzhq1fPU0EvURk8Q9Blg\nmBTn540cT58+e8IjyG9pQCa4iNDQdSpKJk3YPtYD3/0NlrRwceOPSeLg0tHbE6sFj0Rpbe/iM1/6\nNn39g2c8lnJefB94QUo5HZhHrO/+PwFrpZSVwNr49wghZhJbzGoWcC3wEyGEnvCoiqIo7yAqOCvn\n3PLUaXy34i4qfHkYQqfQk8G/THofH8pZAcRmNx9ofJywO1qPK5GEXYv/bHoagN6mQZ68fzN129oY\n7gnTXt3LS9/bQ/X6pnMyxumrSnj/f1zKnGuT4doB3IuDHKeB3zz1NC8vup2Lk6/HiweDWFbQ4hG0\nRk+hywgQ0Uzqk4v4+qJP8RWPzt5gEClhRcNRvKInFpTH0lyWvtKL/9sDDA6FEo4pIuBHCxppLmlC\n7OhA/14Pxk/7EIfiM8ca9GUEGU4OMahPBsDG4dXQDnbNaaV4Uj7ZGRkAbN19gHurBwlJQTSenh0J\n/lCQOVW70XV9pMOJoevMqJhMfnY2AD19/RyqqaG+qQnHHa1Jr+k8ccYql5Mc1+H5VzafxZ7K20UI\nkQZcCvwPgJQyKqXsA1YDD8d3exi4Mf71auAPUsqIlLIeqAGWvL2jVhRFufCoUg3lLbEybQYr0xJ3\naQi5UTqi/QlvqwrGgvGuR49hR5xxk7521GH7b49QubIQTX9zn/mc7i7CD/wLh6cuIBJIAWf0eH1l\nyUSjmeR4PkFfz1FK249wzfAhTMKsnfMh7ipYQpY9SNBMIq1pM8HhYXY6Pu6OV0H8cO2/83+v/Cy9\ncjIg0fQg19QfpmLY4kDYYseuI1y2Yh6GMWZZbiSv5B+HgTDmg/0QlQgJYtCBJ4ZwBl3kxX6QsT7P\nbZemIre0I4ISS9rs3rGL3Wt38IOMx7jjfdfx0988Tjgq+DsmcYPop4Io9dLDPtePcaCZG2e7pM+e\nieO4TJ40ibzsLKSUvLR5C/VNsddACIFh6Nx41VVkpKbi0z1E7NeuUY9ELNo6ut/U66Occ+VAJ/Ar\nIcQ8YBdwL5AnpWyN79MGnPyVRRGwdcz9m+LbJhBCfAL4BEBJScm5H7miKMoFRAVn5W3n1Uw8mkEo\nwYWCmUYyAO1HexNexGdbDsG+CMlZ/jd8/lA4TM8/f47BcJjQ3CQ4tXTBgOFKm6ZwJp9rq+KS0Hb8\nMjbru/TQrznSv4PvT7sNSzOx2mpwHJd2TJ6SqbyXAfIGB/jN09+k3ZdKY8oUip0ucvqacTWNVR6N\nR2wvr2zYy8L5laSmBtCERq3XoSG5H/3J4EholgY47w7gzvfGfjckJf6QScqQnxVd+9h6XyH+HwWx\neyOIgdiT1d3bz48eegwZf/J6MPi1zIo/lxIQ4MCBP7zInbf4+dhtq0ce9qHaOuqbmrCd0dlyy7Z5\n/tUN3Hr9u7l++SU88uqL2KfOpp/C7/cyf/bUN/z6KG8JA1gAfE5KuU0I8X3iZRknSSmlEOJ1X90p\npXwQeBBg0aJF6upQRVH+pqngrLztdKHxwZzl/LFj07i2dT7Nwz35qwBIyvAR6k8wuyl5U6vmHa6t\nZd+a51nZ2Y6TnoU4TXs8UzhU9B3n0pZt+JzRcXgci5knqhClPpxUA907GuB/I7PYI5NYJQbxCgh5\nlnCRVUXmQBu666K7scB5a3c1zdNu5pkXtnFRlo/5V15MtxEbh9ZgczK62O9LRk7zgDlaMx1KskhP\nf5aLqtv5S3Mqh013QkW1laBrRszonsWimM6nBvnjjnWwqIAnTR/TIwfJ0SeG4qHhYfoHh/j833+A\n400tbKs7gC50HOniNT2EXQvXiZ9T08nJzOGSpRedZgxwpKGRPz+0g6RaD47poi8zuPuOq/B51HLi\nb6EmoElKuS3+/WPEgnO7EKJAStkqhCgAOuK3NwNji96L49sURVHe0VSNs3JefL7oelZnL8ErDJI0\nL37Nw915V/C+7IsBuOimCgzP+B9P3aNRsbwA0/fGPu/1Dw3x6s5dmMEhpBAEBvtx9InHsqWg3s5k\nQedBDGdiCNWkw6TBDoTrYpctRR9TNnIQP9+XufzEX4qbNonMwXZ0d3w41x2b9/Xv5bIFy/hS3yGS\nB/uZFdRBuMj02LFkspgQmgFczeGViyN4LZcVh3uh9/Szv0VEmEQEccrUfYlRwHRPOdlaJo0DNv/V\nL6jptdBPU8EshMBxHXRD5/s/+iKP/fTb3P+Jj/HQt75M2VWfRU67AlJyIJAJlStpnX0rze3hhMdq\n6e5m7Vf3kHLUi2nr+EIm4lWXHz/w7Gkfh/LmSSnbgEYhxLT4plVAFfA0cGd8253AU/GvnwZuEUJ4\nhRDlQCWw/W0csqIoygVJzTgr54UhdP6l5H3cW3Q9ndYA+Z50fJoHx3ap39ZKy8Eu8qdn0lbdC4B0\nJZOXFrDinllv+Jw1xxuQUtKbmYtwHDatupEJK6FIyaDr46iVQ7nhw9Z0jFOCr0RnZcNR9uZX0Jsx\njdw5y+g+sAVN05BS4vN7KL+6EO9gN06bju6MD7cCSA/2syN7MesK6+k4bkGZoLJxKjWXHEQ09SHT\n9djVfKcEZ6kJGrP9uAIihobM0hFtE8OzQNKHwftFH1eKIY5JDw/IPGw0TtittNgdlJiFmFNvxNFi\n56izM0nVWjBO+W29YRhkpqWNfF9cmkNxaQ5VNX1EavexusPEp11MQ5LF3qKpREwPD65p5ht3TyzX\neObp7eiWhiZHP2wYtk6gxkNVQyMzS8/c2UN5Uz4H/E4I4QHqgLuJTZ48IoT4KNAAfBBASnlICPEI\nsXBtA5+RUp65RkdRFOUdQAVn5bwK6D4Cug8AK2zzzFe2MtAexI44aIZA0zSW3zOTskV5eJJeu0Tj\n5AIcIsHSgLbj4LouUZ+ffQsvYSg5dUJrNk3TaHdzcaTGxsIl3HX40YnnAJxIEdcdaGZDZS6dJVdg\n5i+hPHiQKf4hLqnfwnC7S1tB1kh5xliOplGdU8mQGeDBWbcR1Uw8rsWU6gY+NnyQXy4pQBzsAH3i\nY9AdlxlNQ9i6YO28LGSxCY8MxkL2mBFKBHnYPCnT2CGTqMeLPeYXTDYOJ6wWkgICGX+uqqJ5lBm9\npGlhTOEihIauC65ZsXzk+RwcHmY4FCIzLY0nfvAXLuv0YYpUEDAr7FCx6wSPLi7jmONL+PoMHQ+R\n5kysT3c0ly8/UYVvEty3PJv5BX6klLiui66rLmjngpRyL7AowU2rTrP/N4BvvKWDUhRF+SujgrPy\npkgpE4bUN+LQC8fpbx3GsWIzvK4tcXHY8b/VVK5MeEH/iLYhiwc2dLK1MYgm4IryZP5hZQ7pvtHQ\nVVZcxL4jR7Adh4aKGZBglTtXSq6bbNDZ4qVpQON7iz/NF3b+ND4LK8GR7PLdRFQLUNgf5kM7TxDR\nJJ2lvXjmW3RGqnk+IKnUCnB8fo7MXMi0qt0jJR+O0LBMLw+VxWa7w0YsYIY1nWOpZSxrzuAnh5v5\n7+VTOFzXRbBidC0V4Uo8tuTGrW388qpiTmQHSEry4KzWcNYNQK+LEOBxBVEkdXgB6McAJAX5WUwq\nyiEStaita2FoOITT24RISUVqAgedZ4MzKDX6KDIGuGJGgCtnzSUlECBqWazZuImW9nZ0XWe4P0JW\nZxrGmNa+utDxSsnsqqOkLZuf8HXyFXmx6xwMZ3wY1lyNPiOZvq4I9z7XxBcru2ltacB1XTLS0rh8\n8WIKcnPO+DOgKIqiKG81FZyVN6T+RAvf+smv2XPgCKbH5PorV/CFj9+K3+d9w8es3dI6EprHsqIO\nvc1DZE5KSXi/sOVy1+NN9IYcXGKTry/XD3G0O8IfP1iCFg/2eVlZTCsvp7q+PtY5IkHgN3SdSbmZ\n/G7ZJH77H7tpbs/mxcC95PtrKXe2EA2HOJ48CU/UxmMZOMLF4wqCZoRnSqqQAhw9G0+DQ1FYUj17\nEW0pucw6soukSJDqvKn8ouJ9tHkyEaF+OPgSdNSCbhApXcDjRh6/DJ/AWVuNFMD1SYjFfnQE5Z0G\nC/bafPUDc+lONZnUkIrUJL0VEL4o3m+6wyb5J4M4gEBgOw5CwBWXLqAwPwvD0HFdl7mzJrNh837C\ntfvxZ+cz7PET8iQh0TjuptKQ3MVW8yV+uuF55h3KpeVEO7m56ZSV5KO7LoNNIQySR/pcjzx/wqA4\nKPnQlfkj26SUHO2Osre2kWH/EMlaEmMbc9i6Q0d2mD4z1gltuXGMpqb+kUsZe/r6eOIvL3HLDe8e\nVzLyeriuS2tnF45jU5CTg2m+8QtMFUVRlHcuFZyV1627t5977vsaw8EQUkIkEuXZlzbS0NTKz771\nz2/4uLqZ+Ffy0pXo5umvY32xdoigdXI9uxjbhY5hm21NQZZNCoxsv3TxIqaUlnKs4Th1jU1EotFx\n5R2maZCZU8y2Ta04h7vJiTiAQWdwGvOHnmPX3GLcGYM0toTp3tZHZ7SbNCOFg0t6sA042bliV04b\n+U2pGFKnv7SE54qnsj+aT5uTwrD0IaIhWPcLiIYACXYEjm2ie0yXDyHBeDaI3BXB+VQWg20Xk3vQ\nz80HYfei42xbVottuuMXKszUWXDVXMqychFAV3c/9cfbKMzPwjRjb/eTpQ83V2Qyq2sT6a++jJCw\nK2cW31t4OwOFNbgFu9G2Bul6IcjLdgNIqKlv5tDh41z/rosxU3S0BNcWu9Jl2DuMs/v3UP4pOodt\nPvdcC039UaRj43ARc5cdoeLwIBldybia5FhZiM2FsZ7fySJMsdE/7iFJKQlFotzx+S/zlS9+kkXz\nEvcHP5327m6eW7c+/iFC4Louly1ZzLTy8td1HEVRFEVRXTWU1+3x514mGrXHVTpELYtDR+uoqW98\nw8edeXUJhveU8CwgJcdPWn4g8Z2Amp4IIXti2UXUltT3WuO2CSEoysvl8iVL+PB7bmBaeTmGrqMJ\nQV5OPlvkHD7wWDNfPDTMLxaV8vj8YjZW5NDnN7HxUj19DtFhiw0btrM/eJgmu42qcA38vAdxYvRc\nbUlDvJxfT5QImmOTyTC5/jbCMt5yrWEP2FHGNatO0BpPAKLVQQ5ZtE/dB0DEa7F1eS22x52wurer\nCQpzMtE1DU3TyM5KY9GCqSOh+aTAQC8rN60hN9KHx7Uxpc3CzoN8ZeuPcfP3QNRFfyGIsEaHaNsO\n/f1D1NQ1k1Lgo0fvxznlejEHlwPLa+jY+BcA/n5NK8d7o0QciGLgoHFATKNnQQpD1/bz0IrJvFp8\nEbYWK1mpMCcunKJpGh7ToKQkj/u++j2O1p2YsM/p2I7DMy+/QigSwbJtopaF7Tis376Dnv7Ei/Ao\niqIoyumo4KyclYjtsq8tRE1PhCO1J4ha1oR9dF2jvrHlDZ+j8pIiypbkoZsahlfH9Ov407xc/cWF\nZ7xfRYaJkWhRDumQ7Tn9Sndej4crL17KJz70QT5xy4f4VVspezolUQdsIYgaOp2pXvLcA8j0gxxO\nnY7UTHbtriZiWzjxOW6JRFgS/anhMecWNFhZPDNcwO4TKWzc2c6WBj/OybdcbxO4p+u3PJE4YSF9\nQ9hC0J4/gO4mfusmRR2Wbd+Mf3gQiIVOIcTIrDrEyhaGk9N4/sY7OTxr4Uh0N6VD+UAzZbUZsQ8B\nWqILLF0aTvSwubmCNfNm0iaGsKVDVFqEZYSX5u2ja3aQsuNdNPVHqe2Jjr9uEbDRqbLy8Okw09fD\n2M9K2ikt8aJ2Hw4O0oTpM4q5afUK/vfJ58/6eWtsbR332E9yXJcjtXVnfRxFURRFAVWqoZyF548N\n8MCGTgQCR0p8BaswU09gDXSN289xXMpLznwR35kITXD5381j/nsraD/WS1Kal6K52a+5vPaMwDAe\n4eBIDRmfgtVwSdaieAdOsO9IDwePHiNqW5QWFrF07hwCSUnjjrGzOUj7QAj0UxbhcF0asxxmdq+j\nL6WCrb2zaW/eM24Xv/AywzOF7OEM2jeEOLCgGat1FUZfMQN42JMN3vQplHUepcm2sA0TUnKQPceQ\nuRpiyEVLlwm3AAAgAElEQVT0ngzh4yeR53tnssA3E2ONjnxRYgmJf8iDTLTAm5TMr+8nVNtMbW0X\nTZMqKKksJS83Y+QiTiklWryTiO3xcnTmAk7goWF/NfnCZoluk9fj0lAgEl48CWBVvp+aQCqOrvHs\nZYtIGujDHxxmcNEGolld3PtMA0mTJtMVdTE0iCT4TGMOg4joLM1sZemsafzh4ABDURfNn44m22Ll\nGdEWDG8eutTR40ORpiQjS571RanhSJRGfz+tZj8B20P5YAam1JFSEo6+9vLhiqIoijKWCs7KGVV3\nRfjGq51E7HhXCSCCD5beCi/9aCRceTwmc2ZMYUpZ8Zs+Z3pRMulFyWd/B9fiptSjbBwqpNFJRyAp\nN3pZ4jvBiVYf1fXhkWWkq+vraWhp4dYbrh+3Ut2emtbEOVE3qDZzOTbvbuirBOnB50QJx2eO07VU\nbky+Cl1oGMJg0i6H/LqZvDirCMnoBWgRw0dL7jRurFvD85WryL1siOqC9NiVjLpAtNjofxhEDI0O\nYplvPrO9U9FE7FxCCjyuJLs7mYyuAJ35A4xph4zXcgm8OsyXnXyiCOTxdqqbuphcVsCUyYXk5mRM\nCJuOYdI3Yw7PHujAlA6/jYJuhpHFBvg0ZHT8yoSpaSV0p8ZC80nB1HTCyank1F5MV/rTrKgLkfql\nr5Ca6QUEhuNQ0TFIWshi0Gcwo6WPzJCFpiWjaxorCsJ88u7JuFKClDzyfAu9/f0MBHzkWeNLd1qS\nBtmb0cr6A9/miqzZfCTvMjKMxD8rYTfK18NPUZ3fjC1cDFdjS04j722cTq6bQnnxG/+QpyiKorwz\nqeCsnNGjB/uwTvlduwR8KelULL2EIzs24TUN3nPNpXz2rg+8bePq7OmhoaUV09ApyMnBT4Qrk2rH\n7WPoOsPBII5j02kdYH/uEK6AuZ0B9lWVsnT+gpF9faFOEOkTT2RHobcJ6b0SIQ0CQ11cxiBrSSGC\nxkr/QkxhjIRbw9FpT05BSmNi/TEaPtviEmMDLxS0xBY3iS9wIosM7LtS0Q5F0femoqdOIlmbDb3j\nV+A7GXxX/2kBj926g+FAhPm7S5h5qIBAEKqHmxDiIFLGZlNt26G2voWm5i4+ePNlCZ9LTdMwTYNo\nNPY6+9Z0Me3iSrRPFdD4o6O48fDsSklZxSyOSDmhMMbVNGwnHQyD3fd/hvKZsXZ0980M0PDTfeiO\ni+nKkUIMAeAKXCSbHzpERlGA3MoMalu72F3TRZJh4xQaMKYi6GBaO9tym7A1F6wBGtu7eap7B4/O\n/PuE4fnhtnUci7RiabHZfEt3saTL2sI67g1dSWlhYcLnQ1EURVFORwVn5Yw6gw5ugplYXdO4+45b\nuOxfP/q2jkdKyas7dlJdX4/jurFWc0JQWlTEiZaWkZllQ9dJCQQYDAbZ6tlAVYVBxBNrldeSEeFY\n4y/57Zy56PElt6sGqpCtGYj86WDEZ6IdGxkZRHp60JAkR4IsaTrILaKXIamzhSQKjdwJs7h+y8V0\nLaxTyj6EFDSJpVSs7+eujcVsuKyaw3NayYj4SY166UkPE5x0BaQX47qCdbbAY7u8d18TqeHx9dC+\nqMmHH15G1LQxLQMtntKneiso9hTxyMBz2PF46ziSwKRKpEzYgQ/LsolGRxOqHbL4YcE95M3J5PCk\nWn73xHNYtkNebgbhqMkhd+JBNMfFMLuJGILejDFlMGvq8dnOyAWGiYorHMvl4PPHaak7wo9//N9I\nKXEcl5mfmUJOOIApdSzhjIbmuKi06bOH+W37ej5XdP2E4z7dvYOIPKWOXEC/N8KyhQtGSlYURVEU\n5Wyp4Kyc0SWlSexuDRE+pWuF5Urm5iVeHe6t1NzePtqHGQiGY+HnREsL16xcQXVdPVHbprK0hIzU\nVB5+7pfsn2biGKMhKeLRqcuCDXuf5fKFNwKwrvgocksP9DYiShaBYSJbDkPLZtwPz+Cjf36B1Y3P\nINGoESb3iQ46MNiJDYzvCTylY5Cd5QlmrxGUdYUwHAPDhktfncZsbxYpeHCFRHd1Ttg2r7oGEoFl\ngK1pvDSjgJv3TOxWIhB4rfHn1oWODw9TPKUcicYuftMQZGTmQLzGeWzQt2ybXXuPjj+wHvvgATAU\nDFFQmMVx0U1UuAT8Id6lb2RnuISOUFlsfynRpaRrxla8msnc5FIA7IhDx7G+cY1DIjLK0Ug9HU4P\nmXoa0z2T8Ws+hnpCPPjgQ9j26Fy23FNDz4xcMqIBer0hEpV1W9JhQ//hhMFZkrhGWxMCoUKzoiiK\n8gao4Kyc0Q1TU3nkYD8tgzaReMmGzxDcPi+dDP/bvxTy0ePHsR2HoUEfck8K6YOxmdL+ZJNjBcPU\np2fwm32DROuCJKW0EKlsw0mwdHXYo7Gj4wCXcyOW4xD2WnBrMtr6w+g796BHJe40k+jHA6w81sjq\nxj0YJ+sGpJeoEOQLmxJrP03mXFwxGmA9tsvi/VvYOzu2urFE4GLyrkOteJ0xfZpnRMlwfAhNjITL\nSXo/czyt7I/GygikJuhJ9hA0dZKsWKiUQoLHRUT0+OLa4x+fKUwK9ByOEAvOPo+H5eWe+Gzz6L5S\nSvYfqOVoTdPoNgHpRWlkZcQWGslIS6XJ209xNAPTjb3eebafa8w2XnQF3cFJZPT3MTR3HU5GkNlJ\nJcxLKuPR+o00RrpJZXTWfcgd5vHBF7GkjY2DbunsDR/m5oyrCfv8WNb42eGqzRKyqqmqTCUzkoyj\nTWzXB5ChJ14Y54asRfyq7WWiY2adBVDizSbHTE14H0VRFEU5ExWclTPymRoP3TyJPx3qZ23dEKk+\njQ/NTmdFyen7Kr+1BLYt8G9OwmtZI/0U0wYtfrO5mqrMKQiZDcCApwWpi4T1AablkqHH6mJNXSd9\nKIm+lCDuqiTcVUks399Fa5bGCS+8f2MHejw0RyU8IPPIlRa3a72UhtfRreUwqBdiGyZCwqA2wJ7m\nV5l85S4u3wKZvV46o5ciGV1VUWoSmW/FQvPYcQnJdLNjJDjHdgZbi82gyiQXe/4wMtlleC2kuqkY\ncvwxbGkz4A5jYuAiWVW+OOFsrRTgXZqG268j2hzQQHg1bvj0KhojXTzauYWmUCel0RRMOf5Dki41\n5niOsPaRX9NtCvIuruADRddR2pXO8vX/iO2T4IHVRQspbspEk4Itob2EZWRkHtiJ/7c+tIP0lBsm\nvtK+NA7Lj6Mfc+inAxmwIdAJ2pgH4xgUDC2a+OCAu/OvZGP/YerDHQTdCH7Ngyl0Hph8e8L9FUVR\nFOW1qOCsvKYkU+P2+RncPj/jfA+FaeVlbHq1jyxXntKEXHI4ZxLCHp35lenHkXriX9cjwO5Kp7d/\ngIy0VD6d/C6+bT0VW4nP9rK5soBf/WAfHZmCqb3BkeztIijA4hB+vuT6YxuHNpNlZJBWfhm9pVOp\nWP/vDM30s7/Ux54KiW4JPvZTHY81/vwJC34BU4yfWfUbUbxXdMeie/wd6zoujRUtlDbOJyVkj1v4\n2tVNzEAOl+opTDIKMAxwCCY4k8RNAvvjaYg9YfDrmJVeKoqKeH/Vd7BdF39Up5TZE+6pIcjSkuPj\n8/Ktoo+Qa2Zw7Y77sWcYYMQe3EvXHeJDv7uIScMdNFrNCYsn2iNdiJQiTI8H2w6N3pCWB66DY/ro\npQSjNht7yvPIpC5wNRASreliGkQuJGj17dc8/Hb6vWwaOMKh4UbyPOm8K2M+SfobXxZeURRFeWdT\nwVk553qbhxjqCJJRkkJylv+cHrswN5ckUtCd8au+2QZIO4AApBFE+nqRjjmxMTKAlLyrLhsXH1v2\n7qW8cBL9RzqZWZXHkcK5SE8ZSMH/WdnPQy/9A/qYxbx9QnKP6OY+WQQI0rLTuThjAYV9mUSDNvui\nx8jQQGRp2LoLCBxTsmVlDcs3TMGMrcuNdCUyKBDJ46OkK6HFjpUR6LgIJOn6MN0iiWx9NPzqukZ+\nYS7PZRZw6ZEuCvpjgbPfb7JuWh7ZQ9nMO9YZO1eHi5MgpDtCUpvaA5pALvSDlHz8uWG+43+SsBtL\n+SFDni7f0y9j55QCpk6exEOPvkAxU7j494VkdQaQHomR28IV3T8FCV6KsRKsuaTpGivLU3hx6c3Y\nG/84cnGgFhnA0UY/Egg7CfPI+5DefqQRQoSyEK5JdpnBrpYQfz46gCvhXVOSubg4CSEEmtC4JG0m\nl6TNPM2jUBRFUZSzp4Kzcs5EgxYv/scuOuv60XQN13aZvKyASz4xBy3BKnSvJRyO8NSa9by8aSep\nKcl84D2rWDJ/FvMXl3L0wAH0MW3yTBsW17ez49JDWDk14Oqg2bFUN6ZOQbiQbvkppAKA+qYm/v2/\nfkM0auEKAfuPIOZdCyUXsaxtD7amYzjjm6/9WOYAEEhL5iaxCrMz1tXCYxksqXJom7IKrX0rRlRi\ne2OPe/+CRgZTQrxnvUlJXzutWfBKfoCLhyvRpUCLB8rYRLTLVLODFBEhRQuzPlxBq53OYm8jMzzx\nMCwlutdHWJr8eV4xHttBcyVhjwFSkhEcXdzDdnT66tJIruwnNmceq5OuSu+gwx9f7VBKytuCTOoY\nYtgdvbDR1lyqUjqYMZg7rlzDEg57DtQgDfiXz9/NL55p5NnGEm7Yb2DE27CIiIATudSLS5lpvcxV\nDPBnUseFZ9MwuHzZAu5ZmM3a+kr0d91LaututOgQdlY5SRl+WodsrDGT8CKShojEarB9hsDU4QvP\ntxCxY5cDvlw3xFWTk7n/8okdTxRFURTlzVDBWTlnNvziIB01fbi2HFmOun5rKxnFycy9YfLrOlY4\nEuXuL36NptYOwpFYCNy6+wAfvXU1d7z/3ez70zG0ntBIiYJA4BTsw82sB80FLR523diFd6arIQWk\nWB7e3TR15IK64WCYcCSKoessXTidKZML0XWLdvsg6SKExxm/utyQ1GjAAwjmFMzE6NBHWsEBmLZO\nQVsOV2mLWD+4H3SwDQ3dcfn4lk3M7BjCG3WpDAtWPiz42m09pOmlzO9IIewPgK5TavZTavZjS40X\nQ1ORaDjAjkgJk80evCL22HziZAyGqDEaag3pUh7uJegRRHWdwwXpHMxNJznSQmHhdnQBDYE+enzx\nsoj42jb/54kT9M68AkeOXxFya34TFi5zBvMxpMawFmVL41FajUEWfvpaIrKEh1uHuLypH/2U3oWu\n8HDcs5DK6EY+ovVS63o5iheJjotOGinctuI6spIM/vCBEv5wsI/tzRnkJ5t8eG46pWkm/7a+gw0N\nw0hAiw/XowtcCbfPS+fhvX0jF64ChGzJX+qGuHlmGrPPQ+cXRVEU5W+XCs7KOWFHHRp2tuOe0rbO\njrpUvdjwuoPzn9duHBeaIRam//t/n+TGay/nY99czh8/83Js5b24/Rc14pindF7QJFiSFTVF5PhS\nyYj6R0Kz47gcOnwcgKuuWEBOdjpGPIDmGSGcGbn016aTMdw3cjgxpko3P5rJkDXM0ehxIjJKmVlE\nkZGHo7ukpqVy43Nz6ZizgY0zM7h6VyezGofwxadOffGVGP/hsUP86PpBrn22jr1zl9NQORPHMBl0\nTTa0+ujor4OUHEgvQBMuzXYqRfoAUUcy3DvAEl892ymLF3UIDFdS3jlM0YkwIBlMr6MpexHp0T4W\nddSxrTxCd6AP92SHCgmmo/PNhw6RM2gy9yMf5dGe31AVbMSNP1YpYF9+O9mlpWzsr2fI04FRmszq\n5Nv48pzLuPmHh7E9JtlDkYRlHRouIS2NVLeTb+qt1EgP2/TZhLyLyNOz2PE/x8grziJnchqfWpzF\npxZnjbv/t64pIGy5hB1JmlejccCiP+xSmeXh8aoBZIIlHyO2ZEPDsArOiqIoyjmlgrNyTjhRl9O0\nzSUashPfcAbrt+4ZF5pPMg2DA4drmFtSiWloI/2cAaKe05xHh51PHOTG61YikkajXWv7AIePNJCR\nnjwuNEN8oRAJu2Yt57LtL2ISO7aumxTqOk225HColprBOiQuLpLqaD3FRh5X6stonrWPrXODzD1u\ncse3a5lth/CJie3UkiIOd6xt4zvzP8nW/AVoQzbStohuewQGx8z8puVjLbuVbeESItLAxOWm7CqM\nqh5u6pIcz0zH0jVKu4fJHwgj0HGli94S4Is1X8LOqeAbS7+APOqgFe5CZh9B0yxKh1NZ0F7GcEUB\nRV+/h7SsdL6bcSd3Vf2QtmBv7CXVgEMhDm3YwjP/9RUy08e3cuuLx+WegIfUsDUhPLto+N2Bke/L\nhKTNN5s+Pdb9xLFc9j9bx6rPX5T49SPW3cUXv+6zJM0DsUoN/KaIlQGdMtNtaJBkqjINRVEU5dxS\nwVk5JzwBg+RcPwOtp3RvEFA8N+d1Hy8rPRURX7BjLCklqSkBPAED95SlwAub02ks7Zl4MWCHQzRk\ns2btDm5+zyUAWFLQEgmgo5OaEsB1XWB8yzVDg4P+FHY52dxjODiGh8enXsmkikJW6N08+sS6kZIU\nABubJruNfYFqds8ZxjJ1dpVkcgCD73hawZr4QcBwBS9lv4e6pBlM7gjSG/DQcexl6O8AOaa2uq8F\nDr3MvXY7F7XvRaJRlz6PRu9i5JAka6h3wrE1oZGpZ/Ov5nTcRX8HwgBpoDUvR2tejonD5cl7EcDc\n22OhGSDfk0HJ73W6BgdxUwRao43oc+nSdX7wP3/gK/d9Ytx5phiSEwMhfNapC3GDwKbIOYhJJP4c\nmbQZlfRpReP2G2hL1PXjtV1Znsx/bu6asF0TgndNSdzfWVEURVHeKLV8lnJGUdvh5SNtrKtux7In\nBqOThBBc+vE5GF4dEV9wRDc1vEkmi2+Z+rrP+/4bVuH1jF8VTwhBWkoyc6ZX4E/1UjgzEy3e9ixs\naMzaPhvT0uHkMB0JUYnxTOwCuOBwGIhNTkbROXDZMWb7pjI4EEy4/LJtO3R19rAZPwftCCeYgju9\ngIqkITq7+nATrEVu43DIqiLiiYXw9D2zYcWd/GXq9YRPWYIbIChMjL5pXHOwgxU1nVy/twmt6dD4\n0AzgOngadrKsdSMBt59kt5eZPRtZ1PknpM857Sp5EpBFMxOutS2BBjsDgSQrebT7SXt9L9l1OdzW\n/S5uqFtG/mCsDaHjOLy0eQdBJzLuOB+fncbqfc3kDYRjFx7qMtZz2pA4lTap1+cjFqyk1ZzGHt9q\n9vpWjxuPpgsKZmQmHP9rSfPpPHB1Pn5DEDAFAVPDqwvuvzyX/BTztQ+gKIqiKK/DOZlxFkJcC3yf\n2JTdL6SUD5xyu4jf/m4gCNwlpdx9Ls6tvHWeO9jCNzcP4MYX2NDX9/LVS9O4cnpBwv3zp2dy0zdX\ncPCF4/S1DJE/NYOZ15TiT3v9fXNnTZ3MFz/5Yf7z579D13Vc1yUrI43vf+2+kZB7+Wfnsea7u3kc\nk+rcFHRXoh+ZhAysxfE0Itod9E0hRFdsVjgtPQVLajRoOluKD2KbUdKnz2dyRi6hcIQkvw9djx3b\ndV0cx6X6WCMe4HDSuylNK6BAH0IIcFw3YW0tQGTAQbTZZD4OQ727IOU4L01byZKsmczrrkJ3HWzN\nwJUuD5d8GOF6yAxa6BJMZxCJQ6Imz66U6IwGagObLLuRZL2R1pIsfG1+PNExb2kh6fB3I1KTkdrE\nt7qLIOia9BrZpAe8bOw/zG93rWf+w8WUmUVoaKRoAQqSc3hpeBMn7FYiWFy1/yv8rPKTzE0uIxwM\nUfunPZjuaGNq4QgkEk+Szm1fugEz/gFocGMz7T/dP76kR4Dh05lzQ/lZ/mRMtKIkwJo7ytnWFMSV\nsKQ4iWSPmhNQFEVRzr03HZyFEDrwY+BqoAnYIYR4WkpZNWa364DK+J+lwE/jfysXqJa+IP+2aRB7\nzI+IJeH/rR/g2eIMMpMTX3SVVhBgxd2zzskYbrr2cq69fBmHqutIDviZVlE60l7MtV32PVXHGkvn\naGEKjqbhaEA0DT36XsTRjYjDG0aOJU1ovdHll6XbRk/gGATQKcjNIqgFaa7rIac0BV3XaW3rZtvO\nw4TDUfxoLLb2ML/rCbTHLDrzirGmzE84Zgk4C30YD/YzYMc74YX7cXsa+fqim5lWeT2zu6vp86Sw\nKWM64RMHoPcv6CnZXBuaxE3B55hFmEP4GNtBWSBZkGARk5fmpfPza2uIemspbQtyyS6dkqPT6NHK\nwC/46P3Xca0e4L4XWgmdcuGmiLfTeGmghKmt2/he6+Nc98JcDGtsrbfAxGCFfyENw88iCw1CL/fy\nmdof8bv5n2P4nz9LxLgLRNIpxxa4YYgOOZiZseA8ZWURxfNz2PXoMU7s7sC1XYrmZLPwA5X/n707\nj5OrLBM9/nvPObV39b7vSzqddGdPyMISQmIghB0BQVFQvCjKHWe8Mwqj4zY64p2RO644joroiCwi\nm4BAIAECSchG9k466XR63/fazznv/aMqvaQ7bElIJO/388mnq06dvbvTT731vM+DL+3dT+LriQ3x\nUOd6tg4fosSVxc05F1LhyWVZWdK73sfZSAjRAAwR/0zGlFIuEEKkAw8DpUADcIOUsi+x/t3AbYn1\n/05K+fxpOG1FUZQzyskYcV4IHJRS1gMIIR4CrgLGBs5XAb+T8SG6jUKIVCFEnpSy7SQcXzkF/ri1\nhclaX0jg0W3NfG7plFN2bNM0efOtvQwHgsybOY0Fs6dPWOf1+/dw8PVWdiwoxdSP7SFoQOkiZMMm\nsGOQmoZ5mUSWaGNXwmF5+fq3LqehtYU1/70Nud/Bw5tewWT8JMOvam3MtiMYidHe7LZGrulqY7uW\nxX7bFQ+WAYnAXuJCNJmIGONZMdj1AvtX3sn+tCkw3Auv/gosM94dr6+ZZ8ROltLKFzWTf7LziSKI\nouHCxonkNq1/3C63VCTz88uKMHWLrz98iHn1g/GSbXInhgUHiubT0V/EgpkzmZvnYVNzcEwREolE\nsDVajMcBP257mrCMkdORzGSSNC+GNDAbY+j1McKOMLVPfoOayCAebYCY7p10O1fS+HQJd5KT8z5d\n877fXLVF+7hx770E7QhRafLWcAPP9m3jRxW3sTj5vacEnYUuknJcvcG7gJeklPcIIe5KPP+qEKIa\nuBGoAfKBNUKIqVIem0OkKIpydjkZgXMB0DTmeTMTR5MnW6cAmBA4CyFuB24HKC4uPgmnp7wf/SEL\n65jJchD/eL//fVTJeLfqDjfyxX/+v0SjMSTxIPqW6y/j9puvHVknEohxcH0rVswmakz+kbxwuJBR\nGzmlBPOGGCKQB1YjR1uMFDWmcuNbi3j0wdcY1gOILgeljgI8wsWQHL2+YmLMFGGMMZMANcAwY3xX\ntBHRYIP0EUDjxRkZ1K304fh+7+QXF+yDwAD4UmDPixAbkyssbZA2PyeDn+rN/JfWxBrp57B0UiEi\nLBNRfJocl+bwu+UlRJw6161vY1794EipO4ivVrV7M9Yve+BHv+aHq/L4/EP7qe0eQpMSPWwxnJqY\ntGmEiMj4xMWQJ4YjNvG/BUvYWNIaeUNgmFAz0IAubaZG17PdfRWWGM3h1p0aVcuKMJwTf4ZOxE9b\nnmPICmIlboSFjWXbfOvIwzw34+uq4cl7dxWwLPH4AWAd8NXE8oeklBHgsBDiIPFBkg2n4RwVRVHO\nGGdcVQ0p5S+BXwIsWLDgOAXOlFPt/LJk1rQMYR4TPGtIllakHmerE2PbNl/6xr30DQyNW/77x55j\ndk0Vi+bGRykDvWE0XWDFIHM4Qrd/ko/5+9sRlgl1TRDOwpXeTMFwPqndbi5f00h/Xw1hEQ9cZaJv\n3+bwLoZkYGQXBjolBIn/moyviKERvxeGgI+IYQDOPxzi43oG5qVeMATGEwHGVqCTgHjzIVh2O3Q1\nTHoPmnAQkoJkYXOtiLcVt9FoMmp4rGgKmTKIbkWJ+Syas0wgxmVbu8YFzXD07QFo7a1ENr3O/R1D\n7Cp6Dat0dL2av5azN28F0nShC4EpYcvCw1ywbupIa3CAmGGxJ1DHuKh9zMNcs47qyIvUupZjJf5L\nqbqwgsU3T5v0Gk/EG4O1I0HzWD2xIXrMITIdk4+YK0D8u7ZGCGEB/5X4vzZnzCd/7UBO4nEBsHHM\ntkcHOxRFUc5qJyNwbgGKxjwvTCx7r+soZ5CV03P53fYe6gPOkeDZwKImOcLiipx32Pr92VV7iEAw\nNGF5OBLlX379DN/8SinnFfvwZ3lGKlqcd7CLZ2YVYApA08C2MaTkysMhCv3L2RPZxasdyVyaVU5W\nm8aS5//MrtDV2GI0heBo579iRx7bI6MZRll6OoPJGeysmkZbUTkCSWbDQUp2bCbPCk84z650R7yq\nxHw3+vMT85EFIAN9iP42MJxgTSxPJxHU5SVR1RHCJU1MHESFh8fKrmbt1NJ4agegGwb+9i0Ei7bg\nsCbWhx4RCdO/8TV+vXiAmGv8p+y7Vx+i5Llc/umzF/Mqi/lz10b2zGrBF3Axb3MpUpM4bYPe6cNs\nfmPnuG1NKdnhL2HW0BEMaVMS20FRbCcBLYWmmkWc++krj39OJyBJd9NrDk9YLpF4tIlVS5RxzpdS\ntgghsoEXhRC1Y1+UUkohxHserFCfEiqKcjY5GVPPNwOVQogyIYSTeF7cU8es8xTwKRG3GBhQ+c1n\nNk3TuP/Gam6rMShxhyj3hPj8LINf3FBzyj4OD4cjx91331CQu15s5w87+nC4DWauLsXUBbmDYa7e\n3oTe3YxnqJcpXUNcs62ZrCGbiJ7NVM8F3NM+ndS94O3rIbW3l5CYfFQyU08beWxgsDrTwflLK2gq\nm0rM5Sbq8tA0pZptK6+atPjbfatKkJoATUCPxST9TuKtwId7oGwB6Me8b9XBmu3iK5+eyg3/NJu/\nTJvJ9qTl/NfUm+JBs9DiAbfhxEJjsHM+RjiF16anEdWP8z0xDLYM9yVmKY4nhSQ1+whLinx8ufBK\nrs5ciFMz2Hl+Ew/duZGUf0jmU7/4CHffdQN5hRNrcd8X8zPgSiZouLEQRAwXw34fC/7xzsnP5ST4\nRJSs7zkAACAASURBVPZS3McEyA6hszSlGp+uugS+HSllS+JrJ/A48dSLDiFEHkDia2di9Xc92CGl\n/KWUcoGUckFW1nuv2a4oivK35IRHnKWUphDiTuB54uXofiOl3COE+Hzi9V8AzxIvRXeQeDm6T5/o\ncZVTz2nofPb8Cj57/gdzvFnVlVjWJHOPdAcUzCBsSu7b3Ms11SkM1njorIXcIxbp4QjLO4aY3tVE\nRM8et6ktnDRsHKTtnC4K7ABoNrZuoVsT3zOG7DBTNScXOQtISi6g1LuJHe5pyDEBrq7rhJKSacot\npri9ccxxYH+Bb+S5LHUgD8UQx6aDSxsaNkPOVFzpucR6WtF1jZg0sUscmFf6wCkIAz+5Pgn37iuw\nYz4mJ6g5vITX5lss2f8GacPRRCvvsffOYNf0Cizt0IStLV0S9cRP0CF07i7+KHcWrGZd/25AsNA/\nBWeilNy9d/89t//TvxGNxeKl+9wu0vKyKPj29zmw5jVCTU34K6cy65KlGI5TlwF2Q9a5HAq180TP\nmziFgSktqn2FfKvkxlN2zA8DIYQP0KSUQ4nHFwPfIT6ocQtwT+Lrk4lNngIeFELcS3xyYCXw5gd+\n4oqiKGeYk/IXTkr5LPHgeOyyX4x5LIEvnoxjKR9eHreLu+68he//5AEisRhIidQdkJIFJdMQgKEJ\nXj/Qyqa3duIoi2JOiecpFwKxpydvohEVfg7WbqZsbjmGZTGcW4u3Y/q4PF4TC2kPsMJ/BTY6wajJ\nzpKLsRyTBfI6B1NzyWprwokkikDqTpymPdL4xF7gQn8jhAzIkZFn6QC7xkXuAY2efa9w3tLZZKSV\nsy/Wzq7yLsycY4J5IRHZB5gRW0xtdwTzmBFsicBlOlnUN51NKyuZsm871bs3j/sYyX/rHaxeOIdH\n63/OsT3RjZjGkszRShR1oTZuP3AfETsxMVNa3Jy9lC8VXk55cQFPP3Ava157k46uXqqnlrF43gw0\nTWPhdZcd5zt68mlC42sl13F7/sUcCLaS70qjzH1qUoc+ZHKAxxOf6BjAg1LKvwohNgOPCCFuA44A\nNwAkBj8eIV4dyQS+qCpqKIqinIGTA5Wz22UrzqeqvIQv//IZWvvbseYOY8+Kgv5bxEAxsaYVNNTX\nk8oQrXYyyVpkpAmdkwBhUibs05BhDrd08rLLyWZXCRF2MXBBmEW7qkgZ8CIkWJlRUtuyRnKfbZzI\nIGAGJ/yWmJbN40M6z9t5zBAh+jUXb150Fxfs+hmvzkom6tDArRG7IxV9bRCtNop0CuxFbrwzc0iu\nWMlnNj5C0G8w7PfiSfVhZfVybGCLZmGKIRYXeqnriWIe87qGTZ7sJhqNoesaB6bPxRscpqR+HwOu\nFDy6INntYnZ2OXN3FvGWrwnTGY++jahGXkcKn78iHvTa0ubOuv+ekD/8x671zPdXcH7KdDxuF1es\nvOD9fWNPsixHMlkpaiLgu5UoFzp7kuU9wIrjbPM94Hun+NQURVH+pqjAWTnjTCkr4o47Lueu9h+D\nfnSYVSJTGpHeZ6C5DE2AS5hYCAwkEakznDuIs92DPaYsmiajGOFNFGFS39dG+POp4BIgejkycxNT\n6nI599Up+Ie0cdsBaG0OrGpAs+MTD4lX/ohFTRqbO7Fxs1ckQek5GE4vt73YwoAfdpT50S1JKMnA\nviIJa8w8uUBfBgftNKr6D9Pa4SGQnEpeyE9i6uC44zujkv/1xitkDdTzics/zR+aBTFLYksbLBN5\nZAt7BnfjMAyqp5WQkZ7M7qnz+ZeKO4joTmxNY+mA4Csvr+G79z3Fc1W5PDkrD0sTrBRl3Hnd59FF\n/Lr2BpsZtCZOzAzZUR7peoPzUybW0lYURVGUs40KnJUz0i6xGU2349WTJeS3pDJlfw5Ch0iBQAOy\njCBhWyNgO3guNJ3oNJ1ro1vI7vVg4UDHIjuygRfMAG24CX88CfxafPIeYAP1Uzopakqnenf+hHMQ\ntsC93olrZhuDmalIIWgf6OO113ZhGxJhCmRWGbL6fFK0g4S8Nt94uIHaslw2zalBurJpTOlnW2Y7\nliYREpy+Vmwk+1MrmFO7g8ayKjJCbvIHM2n294Iezzl2RW0q2gJctqseZAP2zzey6J/v4891Jl31\n3aRntxHydxDMmQlphfToJsmyl2ZfIYMR/8g1vNYLgT39fC0aZfWuRlbvSuRlO7fBRddBZjwnPGRH\nEZM0vAEITFJBRFEURVHORipwVs5Ih8Od2Ngg4aIXp1NVm4se00GAtlNgV4Yxy8O4NZst4XzC0kCi\n8eisRQjbIjUcRHMbzD/0KvX73cRSA5ChjwTNR5lOm12zm6jeXQBSwjFVPUTQ4MKXHuOFORn896pC\ngm4Nyl2IHgeOVMGU5mQO+Hvoyavlds+/ooUy0e0YqbvXEj7yFu5PS6TwsKSjiOqBLIQUhP3beXHO\ncua/uIuL/voItTPP4ZpQIb9NrSSQdZDSoQYueauT1Vu70CWAjZBRXPf9hAouoyRmEc6XvJi3gi7L\nhxnTMGI2b1JEqhhfBi9qw9bMGvpcyaRFBkdfkJLw+rX4rv4YADN9xUgmlgFxCwer0uaelO+poiiK\novytU4Gzckaal1TO1qFDpLX4qKrNHe1mJ4EYGAc8DKcN0z7YTWP6bOSYKXFS0+nz+pHCIjA8A6eo\nA4dgkrgQAFOzsd0WWhSwRLzsmzTRkMwOP42Byf8sz40HzQDZBjI73hKl13WAO+6vZHvRuWwp9zOn\ncxe5wS7q08s4nLuA5Fd30Jc9h22aQWvPfi7ID+JL9jAzdYBDl3yM1Ne3MPPNTUxjO+e4DO6b8Unu\n3vYCLvvYhisSX98BrKRLEQjqGgrpLPaNdHc8Wmu7S07M+3XYJr2u1PGBs20jY6PHiAQiLO+ewl9T\na7GEjRTgwqDSk89VmQvf0/dOURRFUT6sVOCsnJGuzzqXP3S+xpS6HIzYxLbNLVYHmohQWJCFM2wT\nOU7bBm/EoMZVSXNfB7GojOc3j6FHNVa/MAsR0+I15QQIaeGz+zgn9Cg+2Y8toCd58uYaXSnxyYQL\njzTzhUM/wGMG0aWNFBqfmfcPHC48L157GWjLncOfgkN83LEXh8dJj4zSKK7BToqffLLVzme3/xXD\nnrx4QUSMlqXbn54yaUv0yViaRkGgffxC3cC18DwApJQ8vXYdhcM+rh2oZl9KFyE9xpRABuf7p/Pg\nvqdxOZ3MqqqiekqFamutKIqinLVORgMURTnpUg0fD0//MmX+HKQ2MSquS6knyefBMHSmOTrRGR9s\nSizs5CaOFLWSa2Qxo6wMx2MBiEpI1Do2ohrV+7NI6/IirNFgUAqdYS2Tna5VxHChSUgfnNjlDyBz\nMAbA3PAzpEX68VoRXHaMVzOmMJRRNhI0A6Ab2C4vuxviJfSGfUnj9jWo5/KW9xrajaoJQbGJg12+\nsQW1jx+8jn3FbQhudjbiNrR4GooQ4HLjvexaHCXlAHT29hIKh5FAWtTDuV3FrGivoGQolabWNoLh\nMH2Dg7y+bRvrt2497nEVRVEU5cNOjTgrZ6RAKIzXdnDbZSt54o3XsaKjeRYxaeLPcONINNqodnbQ\nY3s5YqajYWNLgeXpo0DuIFoqGDg4xDythoUFXuyfvcr+uX7CqSlctFWQ0RXgsCEmxqFC0GOU8Kbn\neubHHmR64xBbpqaO1GkGcEUtztmSgiZjZFpH0MZUxdiWXDH5hRkumvUM5sYieEJJ+Kek0FnXjxyT\nRrI76TJcMZu0QB22MNCkxfrspTxcNYe5R4Lk92lMbR9kc1kGlj7+vW+OT2dOrputbWEyPDq3zE1j\nZUUF0QuKCb+yBgl4ln4E57SakW0i0ei7GkU2LYu9Bw8xv6YGr8fzjusriqIoyoeNCpyVM0IoZvL4\noTbswT6eeeAhDjW0AlCQm8ltK6+h64VhhJZIpbAgFIxgmhaGoaMJuNBzmCG7lR7TiymhL+bDPTCf\nqVYPzkujSC2M1Z/Gctvm6nVHRo5b7zgHzTCxcUw8KaHTZ+TzrUvPY/uMMNVHhmhPc9Hnd5AxGGPe\nDh/e9pmISZKnC0I98cmGx7JizO4ycRyMB+ERaxCha+iOo3MTBZkV6Uz7yi8It7QzfLiFr28Psdub\nh2ZLnq0RZIYGWL67k/qsJLr87nibb8Dn0PiPS/KYljWx9bSzqgZnVTxYNttbiezchlFchp6aRk5G\nBpZ9nATwY+i6Tnd/P8UqcFYURVHOQipwVk67f914gKd2CJAWvpfvIxgIjsSczW1d3POn+3n4x98n\nUB9B0wXF87LpeaAL+5jA1EOUndFyeqQPkFyVthdDiyUKZQjsFBevrbiaVX/5HwwzXvatwNzLfteF\nxz23iO5goG8VmM+ytzAdIW1EzCKrsRR/Uz6ZHUlYZithBB5GB64/3vw6rxdcQEvmFNBGR6lLuoep\nGEhC2AIrHA9WNV2QUuBn+ooiMkqTyapIBSCprIC7X2lmtycPS9M42iW825PCyzMtOn3x4FUTUJXh\n4udXFJDkPH72lR0K0n/PN4ju3o4wHMhYDM/Fl5N8+5dYPHsWm3bsxEy0PJ9YVTqxD9smyes97jEU\nRVEU5cNM5Tgrp9VLjR3xoBlBRvduIuHIhIFay7J57MU1TL2wkCnnF+D0OvjcdatIDQzGh2mlBBvW\nho4GzYI8fRi/FkEXozsTmoZlGDSVVI4sc8kAC0J/wiFDGDKCLiOIMZ2FdRv6jCwyN3yC3LeWMX1X\nCbM3FNMX7ueV8JtsHH6eleE/4sYal+2hC/jZmz9gfsOrYJlgmRhDnVzY2ISwx//a2Zakv2WY4nnZ\nI0HzUTuH/BPSMSxdo9uTDtLC6xAU+B38aHX+2wbNAIM//yHRXdshGkUGAxCLElrzLMFn/szsadO4\n/KJlVBQVkZ+dzZzq6Rj6+DxrTdPITEsjPWVid0ZFURRFORuoEWfltLp3UwcSDwIwgj3Y9sRxTtO0\nONLSNm7Zy4//mbA/BYSgffcAdpZBizcVSXy0NEULISYZM7UcTvpTMwm5vbjDQQSQZTWwcvg/GdDy\nsdDZ6L0JgJgmaEr3cNnOFpLCJpqQWEYJL16ym57yMGKBk7auMKH7wTWx6R46ki83PMG3B+rpO1+j\nfVGYcP0SPMGJ62q6IBKI4U0bn2YR1SevnGEj+MwsHzMKUjm3yIuuvX2OsoxGCL++FmKx8S9EwgSf\nfATfFdeRn51Nfnb2yEsF2TmsfXMT4UgUKSXFeXksX7L4bY+jKIqiKB9mKnBWTquhkBjpWBdNzkfT\nBMem2xqGTvXUeAUI27I5+NoBOhxJ2Ojs2dfAm2/VoqVkYS9dAlq8isWA7cGeJOFAj8XwBoZ4bcVV\nLHv+zxhmDA0bDYnf7mS3ayVSaERcMQJVAYoO2Bjho2co0C2Di5+dyUOf3Eh/epCuDJ2fXFHC1x85\nNGmdC39omOs9LsLPtLN93wDNRV0kD3rQjxl1FpogJdc3YfusWIA2zT+hMYs/GuGOcysnrH88MhKZ\nPOcasIeHJ11enJ/Hp666ikAohMMwcDknL8mnKIqiKGcLFTgrp9WMfI3Nh+LjxH2pVaSmpDDY14+d\niJ41IfC4Xdx45SqsmMUT//IG/c396DIdDUj1zsY1o4JI83bQQkCiZrLlZ9h2kaKFaW/vYtOWfQwM\nBHA7HVzhDOCbk8ra2TdTuWsbWbFGQloyh5xL6DFKEcD+aW34fQOkx1ImBMSaJajZWcDry+owdcGO\niixC3g68wYkBqJTQH5mJLeYy69AweeEn2ZP+cRwxA8PSkUgMp86ST1WjGRNTLb54URrffi2KpWnY\nmkDYNrqEj89+b/dZJPnRM7KwOtqOeUHgnD3v+NsJoXKaFUVRFCVB5Tgrp9X3z68EYQMShMbQ4s+Q\nVVGFy+XA6TSYN7uKP/zkO/g8bnb85TB9jcNI20BIgSYFxUHB5X0ZcO4nyempZ4ajDT0xgvxcsIrt\nbSYvrdvGwEAAgHA0xhNBF9t31hEo8LDbewmvJH2ON7030WOUAhB1mLQWd1J8pHfSc9alhn9oNKVi\nYXcxdZUzMPXx70MtodGhT8EUXmycBPU02jIupT/5Md6a10hX9iDM0Lj07oVULi2Y9FiXzCrjP1f5\nmSr7SA8HKbUG+OZ5Brctm/Ge7rMQguQ7vwIuN2iJX3vDgfD68N/y+fe0L0VRFEU5W6kRZ+W0SnE7\neeKmQr74wiFaelzYTgd5q6/g0eWVtLa109TeTnNnB26Hi+1/Pjhhe11CSijGNHOQc0psDNFCtbOL\nI2YalhTs3rkHyxqf+xGzJXv2HmHWjApkcZiwbiILYhiWjrPRSZsI0lzczbynG3hLnI84phlJ1GFy\npLQn/kRCyXAqh6alkzrYR+GRg9iajpA2A6kZ7IitHskWEVIQDOcw2+XgiaWHqTM6+HPNV0gxJqZo\njLWwIp/ffyH//d/kBNecBWT88L8IPv5HzOZGHNNn4rv6Y+gZWSe8b0VRFEU5G6jAWTntCvw+nvjo\nrJHnpmny+JqX6OzpZcObezh0uJVFjtlUOyvRJmnUIQVU+9swEhU0krQoNc4OMGHPYM/kB7WhMzaI\nmB8gM+LDIePBsZkaItmy+OajzeSE+mic1UD5gSJsEU8BMXWLYX+IA9PbccRsYpbAikkcDo2ti1ew\nd+ZCUvp7CHqTGEzJxPGcZ3yqh4SuqTP4aFYJt+etfMeg+WRzlJST8vdf+0CPqSiKoigfFipwVs44\nu+rq6O3v59kXNtLdM4ht21R6SycNmgFEqkmyOzxumVbvRK/1kG6n0ErnxI0kbC9o5+LeqSNBs+gy\n8Ozy4wlptPIZBlJqeW5VA989UkswOBNLOMkwa6nLauC8fW56Ixr710gOVjUzbWoxhqET8vkJ+fxg\nS0RHPKVk9JASmWEiMnP45+KPnrwbpiiKoijKB0IFzsoZp67hCO2dffT2DY1MEhzbEvpoyTmAmAOs\nhcOMrcYmenT0/R6ELTjHPZO/DK/DYrQ2s4FOjbcSYTkxZDzfVwxqGJt9CPvojgSDVhUXP5vJz27Y\nyL2/eAhD2BhCUr5DUNjt57uZN8OyWWzTBFmxXaQTBRHfnyF09P0upC4RlkDqEnRJbMYw7nDkVN06\nRVEURVFOIRU4K2ccXdfoHxhfoeJIrIVyRzG60BCAKQQRQ6NjuiBHE2hjys5ph10cjZNzjSxW+S7g\njdB2+u0BXMLJwrJMPMUD9A+Eicl0nMKNdtDNsZ2zdUunpCGDfelZ3CZDzFlqkeG2qM33cbD+E+DN\nRegGFvBsdDZZdpA0EWBIuumykygv3sK5uhN9yAC/JJYTImxFObBpD2JBH9vbQpSkOrmuJoWC5Ela\nfiuKoiiKckZRgbNyxqmZUsm+A4cBMJDkE2NvaAtklVOfn4mtG5R1DpDVO0BSuB6DLBiTSSwi2kht\naIBCRy43OC7FFjFeufoF1hcGMTWBYUl2mtu5tr4c73DFuG1G9mUJfHsFLZbktYxk5Awn2uFMdE82\nYmwVDU2ny/bThX9k0YG0efTufYyafC8+j4fm2i72H+mG8z/L1i29RCzJhuYgf9o7wI9X5zM3z3Py\nb6aiKIqiKCeNCpyVM05VWSmL5s6E117jpkATAomhCXaFH2dT6h0EnD5aU90U9g5zZ28t+6x0bGP0\nR9nOjSEG9JG0iyErgFtz0Tz7DQ4UGUQd8XQK04CIQ/JSbh2XphfjGNLH5SQDaFIQNOKpFfrGMOY0\nJ6J/fFvs49IMur2lvPL6mtFFs1cjnF4sKz5Cbtpg2pLvrOvgzzeWjEtJURRFURTlzKICZ+W06+zt\npbO7B5/XQ3F+Ppq0WdJYy4xwE0Ik8iekZFbvfr6z8T/o8maQHepBOnVS+iTefgcR24/0W1hVYSKl\nQRxNBnYI1g1spNlsR0Pgn+0i6hjf0lpqgvZUB3urapnZMgstNn60WiIxqw30Zg2aTPS/BpBV/dD3\nztclNIELG5HoYWgiMIprCE4yst0ZsOgJWWR61a+koiiKopyp1F9p5bSxbJvnXn2V1o5OJBJNaLiQ\nXPL688iGg4gxvbcl0JaqU97XwJTBBjSgTa9kq+dq7LADAYgeDTbp7FrVyo5bd5D1J42e3k5sbCzA\n1lzHPZfsTW5EVEwY8Q2IEK2LQ8zur2DvpkMY203sXQexF3WBPweOpmtIOaEttlPX+K//cx3BrdkM\nDwwy/5KVfOqFQYKD5oTjSylxT9I5UFFOJiGEDmwBWqSUlwsh0oGHgVKgAbhBStmXWPdu4DbiMwb+\nTkr5/Gk5aUVRlDOI+kutnDY79++ntaMT07KwLJuYaZK7aytmYz2MCZr7vQZfuL2a9ICJIUd/aPe6\nP4Itxk+q0yyN8s15RF0WnS0d2HJ0P7k7Ajhix8wABDKGTTzT0ogSw5TxoNaSNjFp8vKS3ZiapHbl\nMDdmX8Z5OXNYkb6QG3b3kdLaAFYMbBtPdACHBi5d4NTjX2+dm0Z1ro8Fl13Kso9/DH9GOtfXpOA2\nxgfYhgbnFHhJcqpfR+WU+xKwb8zzu4CXpJSVwEuJ5wghqoEbgRpgFfDzRNCtKIpyVlMjzspps+/Q\nIUxrtEyclJDfcBDdHD8i+/+uLMUWoMnRyhkWGiFt8lzjzK4kpu3KwzLdFDsFRqyRQRmidr2L3Glh\nujJchF06rqiFbkNa3Xkc9udQcWEL3W9FcA15GPIGeOMjh+mrjOc3Rx0WSRV+qvdPxTbj53FjvURv\nbmTeRyuYfcUCekMmaw8HiFqSC4p9FKZMrJTxsRmp7OuK8PLhAA4NbAlFKQ6+fVHOCd9PRXk7QohC\n4DLge8CXE4uvApYlHj8ArAO+mlj+kJQyAhwWQhwEFgIbPsBTVhRFOeOowFk5bewxo8pdlo+1oQqq\nxfNkjmlYEjEEWypTSApZGIkJdTaCH8y7g6p6DZclJ+xXSMHKF6rRnDEEAulZREl0M0fCW/jFLzTK\nqwI4izXkABzpqeFgzTnoUYt2w89Hlh1kUI+wpqSOiD4a1NtIuFEj434ffS3DCA1sU1J6Tg4zL6sA\nIN1j8NHqlLe9Zl0T/OuKXD43GGN/d4Q8v8H0TJeaFKh8EP4T+AqMKf0COVLKtsTjduDoO7gCYOOY\n9ZoTyyYQQtwO3A5QXFx8Ms9XURTljKMCZ+W0GGgL4HzLj+OIjuW22V1YSCDdxXMlyykdbMZjxUd6\nLU0ggf4kBzuLU8hpzuVA0hxCZgm7CwSzmvtx2OOD53iDFA1bjOY0NzoXMMtsZLk5xEu1fqhNvKAf\ngBqw0GkzU0gunsb/OB8mIqxx+zSEzkX5M6n4bi49DYMMdYXIKPXjz/JOuDYpJR3dPQTCIbLT0/H7\nJrbVLkx2UKhqNyvvgxDiJSnlindadszrlwOdUsqtQohlk60jpZRCiInvRN+BlPKXwC8BFixY8J63\nVxRF+VuiAmflA9ffOswTX38DM2wh0DBCGssHOnh9is26gsXM6t7LBa1vIoUgRiqXPz2NlK4smoPL\n6HRLbNPJvCMDSKAuO4nKzmE0KdGk5HBZF0VN6Wjm+B9tSzhpd87hCusvvCTHDLjZY1JFbOhvT+Wz\nS1byi7YXMKWFROIQBrfmXkSFJxeAjNJkMkqTJ7224WCQp15+mUAwFN+9bTOtooKlC+arUWXlhAgh\n3IAXyBRCpDFavDyZ44wGj3EecKUQYjXgBpKFEP8DdAgh8qSUbUKIPBj5uKcFKBqzfWFimaIoyllN\nBc7KB27Lwwcww+NHdB22ZHF9Nwdyk/nRnM/yWMVq5nQcJK89m8J6gZZojW2PWR+grDuADRgS1q7Y\nx7A/QlFTxqTHtYQD77HtATNLRx4KKXEPR7nKvQBXSFLrbSMnK4OL0+cw1Zv/rq7t+fXrGRgaRo7J\nx95fX09ORjrTysvf1T4U5Tg+B/w9kA9sZTRwHgR++nYbSinvBu4GSIw4/6OU8mYhxL8DtwD3JL4+\nmdjkKeBBIcS9ieNVAm+ezItRFEX5W6QCZ+WUi4SivPzUNgIDYc65qIrWPT2TrqfbEn8kSkVyF5W5\n3fg6MhGWNmlHv6PcZrxGskRSO6MNIQE5cfK/LqPkxPawSSZSK4QOhgNmrYo/tW0M06S7bRtX3voK\nDoeOlODzerj83+bEx/newXAwSHdv37igGcC0LHbtP6ACZ+WESCl/BPxICPG/pZQ/OUm7vQd4RAhx\nG3AEuCFxrD1CiEeAvYAJfFFKaR1/N4qiKGcHFTgrp9TW12vZ8NNatEQRuefWbqVH9pGjZU5c2Zas\nsOtJO2QiHBpav8CqCsc7AZoCrcEFrTpDKRHcYQfuRP1mACnA0m0QsHauzYqtAt22QejoMkqy1Yo3\ntp9HZR4CiRsL3znXM+jxI60oxUOt1OzczTPBPURjMaKxGAChcJi/+8YPefI3//GOqRYx0zzuOkf3\npygnSkr5EyHEucRrLxtjlv/uXW6/jnj1DKSUPcCkudFSyu8Rr8ChKIqiJKjAWTllTNNi/c/24sU9\nLqBMJ5Vusw93ioedc5voyBsgrSuJ6n3FZG3zgKXHP4QWID0R8NtIIJYSoPaCLjZkNSOFzdzNpZyz\nqQzD1tGkIKcthY68AfYv3ExncT6z9yYxtSVMYdc2dkea+ZEsIJQI4ENSUvbG/fwgKYphmyRHQvye\nYsLW+FQOKaF/YIh9dQ1UTy172+tNSUrCYRjjSuwBaJpGeVHRcbZSlPdGCPF7oAJ4i3hzEojPiX1X\ngbOiKIry/qnAWTllNry8G6c0JozCOoSBpdn84dYNmIaFbUhaC/qpndnK1Y/OJ7c9JR4GSDB2eYnl\nDpAU7GPWtvVc09HKgMvFa0mfxLZS8FqDzAq9SLZVz8pfaXz1k9UcLOynr2yQdSWCdVJDfzaG/uax\nZeIEe3GTFmzDIcDEQbvPDYPBCdchIhGav/JFsvLS8X/qdtxLlk56vZqmsXzJYp5/bT2WbSOlxNB1\nPG43c6unn6S7qigsAKrlsTlBiqIoyil3Qq3KhBDpQogXhRB1ia9px1nvN0KITiHE7hM5nnJmT/tk\nNgAAIABJREFUsSyLts4uOnt7J+T1AoQDUY77l90liDpNbCNRm1mXxJwW6z6yb/x6QuJujbDshcfI\nbmtCty2a7QsxQil4ohYXBh4g2zqEhs2G6mQO5xvEHIkfa02CbmGt8iLdk6dQtOHAQmfAm8m5N12N\n2+WcsI4tbaaaw1jNR+j/4XcIvbLmuPekJD+f6y9dxYzKSkoL8lk8ZzY3rr4Ut+v47b4V5T3aDeSe\n7pNQFEU5G53oiPPRdq33CCHuSjz/6iTr/Zb4rG/1UeKHxKHGJl7eONofweV0ctmyC8lIHe3mN3NZ\nBXWPtE3YNiZNDpS3Tvq2rTtrCEu30a2jLwrKm3egW+bI6q2OaqQwKIi+hS5jaInw/NXqNMKuSboC\nWxJZZiD2jc8zFkCSruG8YAXTv/APVOgGT695ncaWdkLhCBoSB5LPi27cR8vbRiIMPXAfngs/ctx7\nk5aczAUL5h/3dUU5QZnAXiHEm0Dk6EIp5ZWn75QURVHODicaOB+vXes4UspXhRClJ3gs5QzRPzjE\nSxs2jMvljZkmT770MrdcczW6piGl5MvtD2DNDLJs1yw0NHShEZMxwq4oTZcOTbpvzdYQ9tjRYUl6\nqD0+0W9kSfz1ZLsTg9Fg2BuxELZEauNHl4WmQ+TYsW/JnGQn1Q+Njh67gd/c+y88v24jr27chnvT\nOlYzSJmIjtvS7upE2jZCO6EPbBTl/frW6T4BRVGUs9WJBs7Ha9f6vqn2rWe+fYcOYdn2hOWWZdHU\n1kZpQQFbhw9xONxB8JIoHeVvMGN9Hp6Ii+YpvVz/yWVcj59fN68hNqattW5qVO7NwbYtTCSaEERm\nDdHbmkZGVyu6jB8z26yjzZjGoMjGxDESPK/e2sWrNelEnONHnaVwMTOUzX6aAYFEMsvv5D9+/P0J\n1+B0OLhi5QVcsfICum5bj9UZnbCOlpqmgmbltJFSvnK6z0FRFOVs9Y6BsxBiDZPn031t7JP32671\nWKp965kvGA5PmtMsgXAk/slxXagNS9oQsBms62VjbzvSKbBTXOyPtvKPJVdzoL+FV4b2olsCS5Pk\nt6SS/4KLjZHdxKwwDbEWYmtjbEhy8n0JnsRxaiJr6NOLaHVOY2p0PRomGpLq5gCfWNfG7y/Kx7Al\npiaICQ+ug5ejXV7Ey8tTOLh1G5lFheRVTnnH6/R94jYGf/5DiIRHlgmXG99Nt56Eu6i8Gz0Ng7Tt\n68Hld1K6IAeHW81nFkIMwcj0ASfgAAJSysnbWSqKoignzTv+FZJSHjeZUwhxvHatyodYSUE+h5qa\nME1z3HJp2+RnZwNQ7MpEiwgc9w2gh6CqrJDy0jxiQYuuJ5sw/k7jU0XL2LKzjkFnBM2GtECEK/St\n3L3odmyXF5DQVc+hhu3c7XbwBdnGlEg3AbdAlu6lL2Umr3bdyKzGtWRFGpBoXLTJyZJdB3lusZ+n\nFubg2/sJqtNT+feL8/B4dGYuX/aur9O7fBXEogz//lfYQwOIJD9JN30a76XXnLybqUxK2pK1P9/B\nkS0dSBs0Q/DG/XtZ/c/nkFWR+s47+BCTcrRnvIiXrLkKWHz6zkhRFOXscaLDN08xebtW5UOsvLCQ\nHSm19PT3j+Q5G4ZBdUU5yUlJACxOrsL7lsVwWHLZisWkpCThMOIpFLGYyeOvruX/Jr9AyB1PhbA1\n2Dd1iG/FbsWOZYFIpEIUz4HiORyyJfcGAziSgzRaGegWWLqgLLWXPeeE2FhUgIgMUtQboTW9hK5U\nF4YN919TSFXq+w+0vJdciefiKyAaBafzHZugKCfHoTdaadzaiRWNp+fYifdoL/5wGzf99CKEpr4P\nEP+kD3hCCPFN4pOzFUVRlFPoRAPnSdu1CiHygV9JKVcnnv+R+CTCTCFEM/BNKeWvT/DYygfscGMr\nP/vto7y19wDpqSlcc9kFuN0OHIZBTeUUSgsKRtbVhUZNRy6d+QapSR6K2hvxBIfpy8imLyOH1pZ2\nnC5ByDG6fzNcSMjOGQ2aj5ISt2miJUVpimVi6xp24ie3wU7HvW8+VtYRBtNc9KaOln0rsn0nFDQf\nJYQAVU7uA1W7thkzMrHDczRs0tMwSGb5sXW5zx5CiGvHPNWI13UOH2d1RVEU5SQ6ocD5eO1apZSt\nwOoxz286keMop19Tawe3/sO3CYUjSCkZGBzm57/5M7dcfxmf/fjVk25Tnp9Pjh3kimcfxDBjCNsG\nIejOymP90kvICvkYcIxU00IEssCepJycEFhOQYudiq2PD6otXWN/bhqLthawYekhwk4dZ8xGl/Dd\n6beezFugfIDkJJNPIV5C0LbP+qkPV4x5bAINxNM1FEVRlFNMzbRR3pVf//FJwpHouEmB4UiU3z76\nDJ+49lI87okjstddvoKuf3gQVzg0UmsZILOrjYoDu3ihJD6XSbcFVQOZVAQFpqeOrY1R+mMOyCgG\n2wYrQgwQnlQmK/5saoJZ9RlU6duoK3BRllLCx869lezU/JN+H5QPxpTzC+g5PIgZHR9Aa4ZGZtnZ\nPQdOSvnp030OiqIoZysVOCvvyq7aQ9iTjAIamkZzWweVZRNLB+Z7DPTI8LigGcCwTMoP7aPliuno\nUuOqxmmkRTwYaBxoPkS/fyk4vaAlRp9NN3TVo4VCWJmFcEyecWowSjTfQ9miz3LHBeefvItWTpuq\nCws5vKmdzrp+zIiF7tAQmmDFl+ai6Wd3KUAhRCHwE+C8xKLXgC9JKZtP31kpiqKcHVTgrLwrhXnZ\nNLa0T1geMy2y0ifttA6miTzOZLqwFsHok0y3q3CEk9kayafd9NHXFYAU12jQDGA4ILsca/Nj6GnX\nYWs6UhMIW6JLyfmHO9AWWkwrKzsZl6qcATRD49K7zqFldzete3rxpDipOC8fb4rKNQfuBx4Erk88\nvzmxbOVpOyNFUZSzhAqclXfl0x+7gq27aolERhuCuJwOLlwyj9QU/6TbaJnZWOnp6J3jqxQGNMFv\nczMRb4QwUpJ4xjcLEw3bsiE5FwznxJ3ZNugO7HW/JHfGlUT8maQFoswKdJI5d4gplcWUFMRTM6K1\nuxn+n19hHjmMXlCE/xO34Zw59+TdDOUDITRB4awsCmdlne5TOdNkSSnvH/P8t0KIvz9tZ6MoinIW\nUYGz8q7MqZnKd/7P7fz7fb9ncDgAQnDJsiV85QufnLBuzLT51fPNPN0cpqDqc9zd9z00KXGbksOG\nk6/H8hg8qGMQ5eCSTKJSi1fS0AQE+8EyQT/mR1MI0pwWfYEe2jbdj8vlIL+8kPJli1hx3gpSB/sY\n/sOvMNvbiLy+Dsx4N0G7v5feb/8TaXf9K64FSz6AO6Uop1yPEOJm4I+J5zcBPafxfBRFUc4aKnBW\n3rXl55/DsnPn0zcwhM/rwe2aODJsmzZ3/HQve5xOTF2jK6Wc/7X0aywN/ZbsaIRH6pIY6oPc1DRW\nXjSfR8JFjEz4EyIeMEv72J3iI8TSGVk83XgQ27YAQXPYy8/aK+j5/q+4qu45dNtCTNLRkEiEwf/+\nMVkqcFY+HD5DPMf5/xHvIPgGcOvpPCFFUZSzhQqclfdE0zQy0o5fQ/f1l5vZ7XJiaaMTuPqzXTxe\nUono7Uff3I8uBB9ZNg+Hw8AVsYjKMcWcS+dD8y5IKwBPCghBarSLSzPacQkfF547i7b+MAfTF9Gf\nWkjeUCeXH/grhm1OcjajrNZmpGUh9EnK3SnK35bvALdIKfsAhBDpwH8QD6gVRVGUU0gFzspJtXFn\nD5rHi5WIm6WrH3PKM6CbyGSBLiAvO2Nk/RnOdjZHijBJBLRCoBXNoFjrZp6xDY9Dw6kdHUUWlJbm\nEIpkYUYLAcGi9u0I3rmur0jyq6BZ+bCYdTRoBpBS9gohVBK/oijKB+DsruuknHTpmkASr6RhJ7UQ\nm/oUaInR4CQNmaEj9NFKG1WOLqY6utCwccSnCJIf62ap8zApLjEmaB5V6ezGQbyrnKXpI8c7Lpcb\n37UfPzkXqCinnyaEGCllkxhxVoMgiqIoHwD1n61ywoaDIda8uomu3n5yCjLIPQSGfz8Hp2wBY3zb\nZOv6JNoe6ENLpHIIAYvcTcx2ttFruanc9xYr977I1sXLaSqpnNh+G5AIsvVhWqxU3sidzy37Hp38\nxJxOEBq+K6/H91EVOCsfGj8ENgghjv7gXw987zSej6IoyllDBc7KCdl/6Aifv+v7WJZNOBzB5XSS\naifT+vcG9jFBMxKS03wE7jRYv+8ASz2VaEKApmHoUXLCjSyrfRFNSs7Z8BIx3UF7YemE4FnHxkqM\nMvd40rlv5if5wq7fIwXoSAzAf9sXcS+6AC01FeFUtX+VDw8p5e+EEFuA5YlF10op977dNkIIN/Aq\n4CL+//6fpJTfTIxWPwyUEm/dfcOY3Om7gdsAC/g7KeXzp+ByFEVR/qaowFl536SU3PVvP2U4EBpZ\nFo5G6aIX8y0PXOgev4GAiG5x86GpdMrXWfXcVurLp/HsOQUEh3RK9+SywX0rhbFdlEW3M3X/Drry\nirCM8YGzJuDSUgePHzEZNDVeKTqXYG4Wq7reoDwWZMqXv4aRqWr/Kh9eiUD5bYPlY0SA5VLKYSGE\nA1gvhHgOuBZ4SUp5jxDiLuAu4KtCiGrgRqAGyAfWCCGmSimt4x1AURTlbKACZ+V9a2nvpLu3f8Jy\nCxuxIzwxcAa8pgOv7eGjO3WcoSGerOrGvbuauXXZOGIGfYbgQFoxqbFFLB/+JcHAfpypM3BoOraU\naJrgokWLqSwp5g4pae/ooXnz6xiREOWX3EJKZdUHcemK8jdFSimB4cRTR+KfBK4CliWWPwCsA76a\nWP6QlDICHBZCHAQWAhs+uLNWFEU586jAWTkBgsnKJgMQtiEmwTE6cU/EYG5vHpbDSWdOPq+Xhtmb\nU8wNa3JwmDr7s/2sn5qNkBIpinjQuBer5ll+W3Mu3mEdp8NJXlbmmPxoQV5uJnlXXPUBXKui/G0T\nQujAVmAK8DMp5SYhRI6Usi2xSjuQk3hcAGwcs3lzYpmiKMpZTVXVUN63gtwssjPTJn9xWCL2RePB\ncyKI1raEKO5LQTNNfIFhFtf2kt8S377H52T91GxMXSNm6Ji6jmX78B28lmnJxZQVFlKQkz0SNCuK\n8t5IKS0p5RygEFgohJhxzOsS3kVtx2MIIW4XQmwRQmzp6uo6SWerKIpyZlJRiPKexGImtQcbaG7r\nxDx0gK/SRhI2bmw0wO10oCEQEhyPDmP8oh/6E6Xj5nr5Q7rFw9FqfpJ1LesKVhKKRbFtmz15KVjH\nVpUTAmk5eKs9NOE8FEV5f6SU/cBaYBXQIYTIA0h87Uys1gIUjdmsMLFssv39Ukq5QEq5ICtLzS1Q\nFOXDTaVqKO/aX9du4J6fPQBSYpoWRVaAr9PGbzSbN6SPbuGgzKHx28wKmlq7kYB5gx8yddAExuHL\nkMN5DNsOhpNTaPHnYnY3Y5lDhJw6cpLRZAEMhO0JyxVFefeEEFlATErZL4TwACuBHwBPAbcA9yS+\nPpnY5CngQSHEvcQnB1YCb37gJ64oinKGUYGz8rYCUZufburmmc0HCK29H6zR1tb1OPgGefxUa2aF\nFp93FDMdtBQl87vOPnLSszj3xXIyB6EpL8gzxbnIMe21TWFAah6Pu7ZR05VMc7oX85jufjEbZudO\nnGSoKMp7kgc8kMhz1oBHpJR/EUJsAB4RQtwGHAFuAJBS7hFCPEK8cocJfFFV1FAURVGBs/I2pJR8\n4S8t1PVEiO3fBNb4v5s2gk4M6nH+//buPL6q+s7/+Otz9yRAwhr2TRBEFFQU0Loi1aIWO9aOraP+\nHK2t3TvtVDtOp06tv1+n02mnnU6dMrVTu2hr/VWldddq3RBZVVYBQUFCQPaQ5G7nM3/cKyQkgcAl\nuVnez8cjD84953vO+XxPbsgn3/tdOI4UAObOCEtz6fCzGbi9L74lQmDGtnQvyEaadg4KR6np3Yf5\na39DePCN0KM3RHLJdSJiXDOpgr6lepuKFMLdXweaLMvt7tuBGS2ccydaWEVEpBFlJNKipVvqWb8z\nRToA6vbQ3LihEM4uGrcS7ygbTOWO/rgd2J9IQThwMgclzrFsilSyBoIs2RfuhuGTqJgwjZPHDOXK\nEyuYNqy0DWomIiIicuSUOHdT2WzAU8/P57FnXyYaiTD7onP5wBmTMDswQm/djhT7exdXjoGdmxp1\n1QBIY4whmbtmOMJ7/QdRkx1AjICgQUI9+r29zBvTr0kcYXd4d3nuRZAhsWUZ377xAqaeOviY1ldE\nRESkUEqcu6EgCPjKt/6dxW+soq4+l/S+unQ5l174Ab72mWv3lxteHiX8fh494lRYvxDq90KQ67IR\nIcyMcIK4lVJrYWIXzGLRgL54VdOW6VjWuXTpOzx7Yj9qozHAKU/t5eaFP+W7mQxZQgQYF3/wfKae\nOrHJ+SIiIiLFpsS5G1qwdEWjpBmgrj7J3Cef52MfnsnIoYMAmDKkhMoeETbuTpOJxuHcG2HdfEZX\n7eAMRtEjVErYQjwNhBPGtZ+ZSfqBB/D+GYJwAg4aSlRZU8ePn/0Wu0siYMbgmmoyOMPGfJR1ZQOI\n9h3GY5GBVD+6me9+cCCJiGZLFBERkY5DiXM39PLC1xslzQ29umT5/sQ5ZMacy4byLy9u5bkN+wji\nJcwYchqjtm6h4ZTLjpM6vp6de/bgQQAhiE2qYvzLS6jIVrM31J910amMyC4iEd5Dj9o06UicVbHz\nWTJoCBvGnUk2Es/l2Vln0eY6fjjvPW45e0CbPwsRERGR1lLi3A2V9+pBNBohnW7cXzkcDtOrR1mj\nfRUlYf7fzEEE7mQyAb/51NMHNyQDYFVh3q7aTGX/ftS9uYpzXnqQcDZDyJ0ewXsMDFbz0rmXsKjy\nLEilyGyMU7qqgn1BnFQk3uhaqazzx9V7+doH+jfqcy0iIiJSTPosvBuadcFZzS5dbQbnTj+12XNC\nZqRr0gSZpv2XDcN2hwmCgJPGjmXSkheJZtKEPFc2hBMOspy85CWy5tS7sXzlOwDEM00uB+SS5yNe\n+1dERESkDSlx7oYGDujLnV+7mZJEnLLSEspKEpT37MEPv/VVShLxFs+Ll0UJhZpvAfaSgEXLlnP/\nI09SvrWq2TLlu7azsqyKhx55ie37dhGOhkiNKqe5K06sTBBSa7OIiIh0IOqq0U2dO/1Unrzvx7y2\nYg2RSJhJE8YSOWjVvoNFYmFGnjuUdc9uhAYtzx520mOTrFm3mVfmv8EVblRY0/bi+miIl/esp6Qu\nw5CySkrK41x17Xj+/EQ1qWxAOoBoCKJh45YP9D/mdRYREREphBLnbiwRjzH1lBNbVTaZCbj92a2k\n3n6DC5PrqApNBEIQDlg4tg8Ly8biJScRmnYy9y35Fden1pPwA8lzfcR4ZHI/ok/VkYjGuepjMznt\nkuOJlUb5/V8P53fLdrFyW5JxfeN8bGI5A3tGWw5GREREpAiUOEsT9ckUjz7zEs+9spg+5T258tIZ\n/HFrT95bvJjblv43iWyKSTxJXaiMz5x/OzsTFTgGoTDebzjPXPj3jH7yG5yf3k4qYsTcmT+ggrmb\nBvKRKVO46W8+Qr8+Ffvv178swuemNl0cRURERKQjUeIsjdTXJ/nbr9zBxs3V1CdTmBlPv7iAzAkz\n+caW54hlUwCECFg08ARqo6W4Hegq74TIWoSFF9/Arx7+HYOSKbb0GUX/Cz/Dk1cOL1a1RERERAqm\nxFkACHbvpP7F53jt1SUM27yX2kwFVWwjcCeZTMEbT1JRuqvRaNKq0kqS4ViTa2UIUxsqo3zIQFZV\n7YSx5zCu9ND9p0VEREQ6OiXOXVyQDVjy4DpWPvUO6foMlcf3Ztq1J9BnWM/9ZZJLFrD2h98glHZG\n7Knj80TYHD6OV0tn81jtC2zNbodshq/WlDHCh3BdaAenWB2j9rxD1DOkrHHyHCGgT7iWdI9SGDuB\nxNBxXH1yxcGhiYiIiHQqBU1HZ2Z9zOwpM1uT/7d3M2WGmdmzZrbCzJab2RcLuaccmed/+gav/+kt\n6vemyKYDNi/fzh+/OY+92+oAWLF7PVds/QXXfXo813zhBL5043i29Q4xOLuOkcEGToyOyV/JyTis\nI863g0oWeAmnbX2dvqk9hAj23y9EQFkoxeDIHvaOv4T4hHO4+fS+TB9W1kx0IiIiIp1HofM43wo8\n4+5jgWfyrw+WAb7i7hOAacBnzWxCgfeVVti3s57187eQTQWN9mfTAW88up5dmX3cuPa/2NgvTjoa\nIh0JsWZwKV+5fjyEMgxNv87C5LIm100R4m7vT2joCOZM2MPEsj3EyBAjw5joe8zu8SZDKyv55mUT\nefK6UXxCrc0iIiLSBRTaVWM2cF5++x7gOeCWhgXcvQqoym/vNbOVwBBgRYH3lsPYvXkfoWiIbLpx\n4hxknffW7eaR7YvIcNCxUIjaWJhXx5Yzag3s9X3NXrvKYgy6638AuCudZvGKFazZ8DahUIgJx53A\nyePGET7MvNAiIiIinUmhiXNlPjEG2AJUHqqwmY0ETgHmF3hfaYVelaXUJ5O8mdxAndczMNyPQZEB\nhMJGn+E9WZlaQ5Jsk/MyYdhSXkIsNolEZgX1nmxSpl+f8v3bsWiUaZMmMW3SpDatj4iIiEgxHTZx\nNrOngYHNHLqt4Qt3d7Nmlos7cJ0ewP8HvuTuew5R7ibgJoDhwzV9WSE27armV7seJpvNkiFLhAiV\n4b5c1vd8TrpkFPviGR4KvUpt0DgxDjv0rerHxshx9B9YwsatCyCb3n88Gotxw1Wz27s6IiIiIkV1\n2MTZ3S9s6ZiZVZvZIHevMrNBwNYWykXJJc2/cfc/HOZ+c4A5AFOmTGkxEZdDc3duufM/SObnXQbI\nkKE62E5wVpLyQWVcEEzkrnUPsimoIx3JdXePpQOGbuvF0u1DWT6hL1WV42FtCf7mixCkIWr41FFM\nuWBisaomIiIiUhSFDg6cC1yX374OePjgAmZmwN3ASnf/foH3k1Z6+90t7NjVtGE/4xmemp/rKWPV\n1fzbD+bxkXlb6L8jS8X6sQxdcD4TFwxnXuwtqir7gxk+7nTSfzeC9Ff7kv6Hcmpn7ODKld/j+d3q\npi4iIiLdR6GJ83eAmWa2Brgw/xozG2xmj+bLnAVcA1xgZkvzX7MKvK8UYE91LRsWbKHu6Ucoq0tz\n1V92UPb6lWSrz2FT7ESeGHwOddOvg1Ruyrps/2VQugt6BhAyCAXUB2luW/8bMt60j7SIdCwtTQt6\nqClFzezrZrbWzFab2UXFi15EpOMoaHCgu28HZjSzfzMwK7/9ImCF3EeO3IghA+lT0YvN1e812h8h\nzLjoKF7+xQpmHb8TMhkeOv4StpX0IZ1fBTAbCgP5GTEyKbzPWgg3M4jQA1bXbubEsmFtXR0RKcz7\n04IuNrOewCIzewr4P+SmFP2Omd1KbkrRW/JThl4FnAgMBp42s+Pd9ZeyiHRvhbY4SwdlZvzLbZ8n\nZlEi+SQ4NziwHxPiY6jfm4aJU7FECS8PnLI/aW6oNBFn1ogwYW/+76sAJxGKtmk9RKRw7l7l7ovz\n23uB96cFnU1uKlHy/16e354N/Nbdk+6+HlgLnNG+UYuIdDxacrsLGz9mJDeP/WuWblxNbYPp6MwM\nMyg7czrZJ8dQGqSaPT8bwE3njGZ6ega3v3M/dQ3KGVAZLWd04pAzEIpIB3PQtKAtTSk6BHilwWmb\n8vtERLo1Jc5d3OmXjydzj5NJHviENRwNMeYDg4mWxOnz7R9y5dyX+NetKepDB1qdQwYje0cZ0ivK\nYD+FRTVv8dD2V4lYCMMoCcX40ZgbyI39FJHO4OBpQRv+/B5uStFDXFNTiIocA2fO+kSxQziklx+9\nt9ghdAhKnLu4488dSs22Ol5/ZD2hcIggEzDy9EqmX5db9dyiUS77q3NZ/UI1D67cTSSTa1Wu8CQ3\nVCb4p2e2sC8dMGP0RVx9wnm8UbuePpEeTO11PBHTyoAinUUL04K2NKXou0DDwQtD8/ua0BSiItKd\nKHHu4syM0648npMvG82e6lrKeidI9Io1KXPjSz/m4jdW8WaPYVTU7+aEnWtIPh1n8bnfprq0Hwve\nrWN8/zg/uXQKkZBamUU6k0NMC/r+lKLfofGUonOBe83s++QGB44FXm2/iEVEOiYNDuwmookIfUf0\napI0A2Sqq0gunEf/vdWcVbWQE3euIQREggyXrX8SgLqMs2pbkmfX17Rz5CJyDLQ0LWizU4q6+3Lg\nfmAF8DjwWc2oISKiFmcBsu9uxCJRPNV4kGDUsxy3++39r+syznPr9zHzuJ7tHaKIFOAw04I2mVI0\nf86dwJ1tFpSISCekFmchPGQYnk432Z+2MOvKDwz2CRn0iustIyIiIt2TWpy7GHdn1VtvsXj5CuqS\nSSr79WX65Mn06927xXMilYOIT5lGctErkG91DoBMKMLcUQcWDIuFjctPKG/rKoiIiIh0SGo+7GIW\nLlvGCwsXsbumhlQ6zcaqLfzhyafYsLqKIBO0eF7F33+Tkos+vP91MhzjjtO/wN5oGaXpWmJBmi9P\n78e4fvH2qIaIiIhIh9OtW5w3Jbdz79YXWF9fzSllo7hywJn0jvQodlhHLZ3JsGTFSjLZxmN4Muks\nT/zpZUpW9uLM609kzFmDm5xr0Rg9rvgEdU/8EVJJSrIp7pj/b6zoM5a6cIKTMlsZdfP97VUVERER\nkQ6n2ybOi2ve4jNr5pAOMmQIWLR3Hfdue4HfnvB3DIy13K2hI9tTU9P8giQhyPbKkKrN8MKc17Ge\nMOLESiLhxvMwhyr6YIkEnkoCEPaAk7avBjPiU89ujyqIiIiIdFjdNnG+fcPvGi0hnfQM6UyWH737\nKP931NVFjKx1srt2Uvv0I7yxch1r4uUMPv10pp4xmSA4qDuGg22LEF4TZ292H0tqV/DTW+8nEglx\n9RUX86lr/opQKNdjx8Jhen7yC+z58XchmUueCYWweIKe136ynWsoIiIi0rF0y8R5d2anslr1AAAS\nqElEQVQfm1M7muwPcF7cvbIIER2Z9JpVVP/DF7m9roLVQYwMRvQviynp1Yu/vfpSdu3bQzbfXSO8\nKkFoQxzLGj3DUaaXTGZkdCiP7fsLv3rgMcyMT197xf5rl573QcK9+7Lv/l+Sqa4iNv5Eenz8eiJD\ntJSuiIiIdG/dMnGOhaItHisNd/zBb7u+fwcP1UZZ6TFS+fGdGYf63XuZ+/hLfOq62axc9xbZPU5o\nfRwLDnTfiFqUgZF+DI8M4p1MFfc++AQ3fmI2kciBt0J80mnEJ53W7vUSERER6ci65awaJaEY55RP\nIGqN+/gmLMpV/c8qUlStk93xHtnqKp7ynvuT5vc5sGHjZiYcN4Ybr7yCUXtGN0qa3xezKMOjuQGC\n6UyGmtr69ghdREREpFPrlokzwO0jruKE0qEkQjF6hBLELMKM3idzTeV5xQ6tkT3VtSx7fAMrnnqb\n2t1JLBwBh6ClRcDMyAYB4XCY8WcPJRxt+i3OepZ6z/XvLi1J0KtHaVtWQURERKRL6JZdNQB6RUr4\n1fgv8mbtZjandjC2ZDBD4n2KHVYjSx9ay5IH15Eb4WfM//UqzvnUSfQaM45zVrzLg15O+qC/fQb1\n70tlv1w9hp0ygFAkRDbdeMBggPNmaj3RUITP3/Cx/YMDRURERKRl3T5jOr50MOdVTOxwSfP2d/aw\n5KF1ZNMB2bSTTQVk0wF/+ekbfGvCjZxbGmIwGRLkkuKoQVlpCXfe+pn914jEwnzo66cT7xklEg/j\nOBnP8GLdQkrK4tz+1Zu4/KLzilRDERERkc6l27Y4d3TrXm5+pb+NfUpZmi7n1RnfZfLW1+m9ZS0b\nssa+viP4xrUzGHdc/0blB4yp4OqfXMCW1TvJpgMGjKngUyWXYqEWunqIiIiISLOUOHdQnnXcm+7f\nWhYn6eAWYnHlZKicDIABG2rDTcrvrqkhk8kwcHxvdckQERERKYAS5w5q9LSBrHzqbTKpxq3OPeoz\nJCJGXaZxVp2IGoN6HPh27q6p4fHnX2DX3r2EzIhEwsyYPp3hgwa1S/wiIiIiXY2aIDuo/sdVcMLM\nEYRjISwEobARjob4+MzBxMLWaE4NA2Jh44JRPQAIgoCHn36GHbt2kc1mSWcy1NUnefz5F9hTU1OU\n+oiIiIh0dmpx7sCmXj2eMWcNZsPCasIRY9S0QZQPLONnO1P845+38NaO3JRyx/WJcceMgSTyU8+9\nW11NMpXi4J4eQRCwYu06pk2e1M41EREREen8lDh3cH1H9qLvyF6N9o3sHePXVwxnZ11uWe3eJY37\nNtfWN7+gSeDO3tp9zR7zdIrUquVYNEr0+AmY+kOLiIiINKLEuRM7OGF+38B+/Qi86YwckXCYYQMH\nNtlfP+95dv/gTjADdyxRQu9/+heiY8Yd85hFREREOis1K3ZB5T17MnbESCLhA4l1OBymZ1kZY0aM\naFQ2s2Uzu773LbyuFq/dh9fVEuzczo5//BKeSrZ36CIiIiIdllqcu6jzp57B4AEDWLbmTdLpDGNG\nDGfS+PGNkmmAumcegyDb9AJBQHLBPBJnndc+AYuIiIh0cEqcuygzY/zoUYwfPeqQ5YLduyCTabLf\ng4CgZk9bhSciIiLS6airxlHI7tzOvrkPUPPbX5BavRxvbqWSTiJ+2lRIlDQ94AGxk05t/4BEpE2Y\n2c/NbKuZLWuwr4+ZPWVma/L/9m5w7OtmttbMVpvZRcWJWkSkY1HifISSC+ex7ZN/zd577qLm3p+z\n87Yvsfv73+60yXN8ynSiY8dDPLF/nyUSlH7wMiKDhxYxMhE5xn4BXHzQvluBZ9x9LPBM/jVmNgG4\nCjgxf85PzKz50cgiIt2IumocAU8m2fXd2yGZbLCvnuQrz5Oc/yKJaWcXL7ijZOEwfb71feqee4K6\nZ5/EYnFKL/4w8TPOKnZoInIMufvzZjbyoN2zgfPy2/cAzwG35Pf/1t2TwHozWwucAcxrj1hFRDoq\nJc5HILV8aW7KtoN4fT11f368UybOABaJUHrhJZReeEmxQxGR9lXp7lX57S1AZX57CPBKg3Kb8vua\nMLObgJsAhg8f3kZhioh0DOqqcUQMmqzH9/6hpgm1iEhn4bn+Zkfc58zd57j7FHef0r9//zaITESk\n4ygocT7UwJIGZRJm9qqZvWZmy83snwu5ZzHFJja/VLUlEpTM+FA7RyMiUrBqMxsEkP93a37/u8Cw\nBuWG5veJiHRrhbY4Nzuw5CBJ4AJ3nwRMBi42s2kF3rcoLBan4pY7cgPp4gkIhyEeJ3H2DOKnn1ns\n8EREjtRc4Lr89nXAww32X2VmcTMbBYwFXi1CfCIiHUqhfZxbGliyX/7jv5r8y2j+q3NOQQHETz2D\nAT9/gPqXniXYt4/4qWcQHT222GGJiBySmd1H7v/rfma2Cfgm8B3gfjO7AXgb+BiAuy83s/uBFUAG\n+Ky7N7NSkohI91Jo4tzSwJJG8tMYLQLGAP/p7vMLvG9RhXqVU/qhy4sdhohIq7n7x1s4NKOF8ncC\nd7ZdRCIinc9hE2czexoY2Myh2xq+cHc3s2ZbkvMtFZPNrAJ40Mwmuvuy5spqhLaIiIiIdESHTZzd\n/cKWjplZtZkNcveqgwaWtHStXWb2LLkJ9ZtNnN19DjAHYMqUKZ22S4eIiIiIdC2FDg5saWDJfmbW\nP9/SjJmVADOBVQXet+g8cPbtrCeTVLc/ERERke6g0D7OzQ4sMbPBwM/cfRYwCLgn3885BNzv7n8q\n8L5Fte7lzcz75UrSdRkARp85iLOuP5FITCvSioiIiHRVBSXO7r6dZgaWuPtmYFZ++3XglELu05Fs\nXrGd5+e8QTYV7N/31stVBOmA8z83uYiRiYiIiEhb0sqBR+i1h9c1SpoBsumA9a9WU7831Wb3zQbO\nS+/s4+7FO3h8zV6SmeDwJ4mIiIjIMVNoV41uZ8/Wumb3hyNG7a4kiZ6xY37PfamAT87dxLt70tSl\nnZKo8YN5Ie6+fChDe0WP+f1EREREpCm1OB+hyuMrsGaemjv0GlDaJvecs3A7G3amqE07DtSmnZ31\nWW5/trpN7iciIiIiTSlxPkKnXD4mNwjQDuyLxMNMvvw4IvG2GRz4+Noa0gf1zHCH5Vvr2ZdSlw0R\nERGR9qCuGkeofFAZs+84k4X3v8mW1TspKY8xefZxHHfm4GKHJiIibWjWf84rdgiH9Ohnpxc7BJEu\nT4nzUagY0oMLv3xqu93vojE9eGD57katzmYwoX+Cspg+NBARERFpD8q6OoGbpvRlREWM0qhhQGnU\nqIiH+efzK4sdmoiIiEi3oRbnTqBHLMSvrxjGyxtrWf1eksE9o1wwuoxERH/3iIiIiLQXJc6dRDhk\nnD2ijLNHlBU7FBEREZFuSU2WIiIiIiKtoMRZRERERKQVlDiLiIiIiLSCEmcRERERkVZQ4iwiIiIi\n0gqaVUNEREREjpkZT/x9sUM4pGcu+tejPlctziIiIiIiraDEWUREmmVmF5vZajNba2a3FjseEZFi\nU1cNERFpwszCwH8CM4FNwAIzm+vuK47kOnfd9Pu2CO+YuXnOlcUOQUQ6EbU4i4hIc84A1rr7W+6e\nAn4LzC5yTCIiRaXEWUREmjME2Njg9ab8PhGRbsvcvdgxtMjMtgFvFzuOQ+gHvFfsIDoAPYccPYcc\nPYecce7es9hBHC0z+yhwsbvfmH99DTDV3T93ULmbgJvyL8cBq9s4tK70/lJdOp6uUg9QXY7UCHfv\nf7hCHbqPc2sqUExmttDdpxQ7jmLTc8jRc8jRc8gxs4XFjqFA7wLDGrwemt/XiLvPAea0V1Bd6f2l\nunQ8XaUeoLq0FXXVEBGR5iwAxprZKDOLAVcBc4sck4hIUXXoFmcRESkOd8+Y2eeAJ4Aw8HN3X17k\nsEREikqJc2Ha7ePJDk7PIUfPIUfPIafTPwd3fxR4tNhxHKTTP9cGVJeOp6vUA1SXNtGhBweKiIiI\niHQU6uMsIiIiItIKSpwPw8z6mNlTZrYm/2/vFsr93My2mtmyozm/ozuC59DsEr1mdruZvWtmS/Nf\ns9ov+sIdbulhy/lR/vjrZnZqa8/tLAp8BhvM7I38975TzzbRiucw3szmmVnSzL56JOdKy8wsYWav\nmtlrZrbczP652DEVwszCZrbEzP5U7FgK0cV+tivM7AEzW2VmK81serFjOhpmNq7B79qlZrbHzL5U\n7LiOhpl9Of/zvszM7jOzRLFjUuJ8eLcCz7j7WOCZ/Ovm/AK4uIDzO7rD1qPBEr0fAiYAHzezCQ2K\n/MDdJ+e/Olq/yRa1ol7kj43Nf90E3HUE53Z4hTyDBs7Pf+87xJRCR6OVz2EH8AXge0dxrrQsCVzg\n7pOAycDFZjatyDEV4ovAymIHcYx0+p/tvB8Cj7v7eGASnfT74+6r3/9dC5wG1AIPFjmsI2ZmQ8j9\nXzrF3SeSG6R8VXGjUuLcGrOBe/Lb9wCXN1fI3Z8n9wvzqM7vBFpTj666RG9r6jUb+KXnvAJUmNmg\nVp7bGRTyDLqSwz4Hd9/q7guA9JGeKy3Lv69q8i+j+a9OOUjHzIYClwA/K3YskmNm5cA5wN0A7p5y\n913FjeqYmAGsc/eOvJjcoUSAEjOLAKXA5iLHo8S5FSrdvSq/vQWobOfzO4rW1ONwS/R+Pv8R/s87\nWZeV1iw93FKZrrJscSHPAHIJztNmtshyK811VoV8P7vKe6Fo8t0blgJbgafcfX6xYzpK/w58DQiK\nHcgx0FV+tkcB24D/yXeh+ZmZlRU7qGPgKuC+YgdxNNz9XXKf3L0DVAG73f3J4kalxBkAM3s633/m\n4K+DW5KcAlo4Cj2/rbXxc7gLGE3uI9Yq4N+OTdTSSXwg/7Hhh4DPmtk5xQ5IOh93z+bfR0OBM8xs\nYrFjOlJmdimw1d0XFTuWY6Sr/GxHgFOBu9z9FGAfnbdrJQCWW7jow8Dvix3L0cg3sM0m90fNYKDM\nzP6muFFpHmcA3P3Clo6ZWbWZDXL3qvzHzluP8PKFnt9ujsFzaHGJXnevbnCt/wY604CY1iw93FKZ\naCvO7QwKeQbvtxzg7lvN7EFy3Raeb7No206rlqFug3OlAXffZWbPkhtXsuxw5TuYs4APW26AdALo\nZWa/dveiJwRHowv9bG8CNjX4FOMBOnniTO6PmcUNf/92MhcC6919G4CZ/QE4E/h1MYNSi/PhzQWu\ny29fBzzczud3FK2pR4tL9B7U1/UjdK5fdq1ZengucG1+Zolp5D5SqmrluZ3BUT8DMyszs54A+Y8+\nP0jn+v43VMj3s6u8F4rCzPqbWUV+uwSYCawqblRHzt2/7u5D3X0kuffAnztr0tyVfrbdfQuw0czG\n5XfNAFYUMaRj4eN00m4aee8A08ys1MyM3Pek6AM21eJ8eN8B7jezG4C3gY8BmNlg4GfuPiv/+j7g\nPKCfmW0Cvunud7d0fid02OdwmCV6v2tmk8l18dgAfKq9K3C0WqqXmX06f/y/yK2uNgtYS24E8/WH\nOrcI1ShIIc+AXH/4B3P/7xEB7nX3x9u5CsdEa56DmQ0EFgK9gMBy00BNcPc9XeG9UESDgHvys5OE\ngPvdvTN9ctUVdZmf7bzPA7/J/2H7Fgf+D+t08n/IzKQT/a49mLvPN7MHgMVABlhCB1hBUCsHioiI\niIi0grpqiIiIiIi0ghJnEREREZFWUOIsIiIiItIKSpxFRERERFpBibOIiIiISCsocRYREZFOwcxG\nmtmy/PYUM/tRfvs8MzuzuNFJd6B5nEVERKTTcfeF5OZMh9w6CjXAy0ULSLoFtTiLiIhImzOz28zs\nTTN70czuM7OvmtlzZjYlf7yfmW3Ib480sxfMbHH+q0lrcr6V+U9mNhL4NPBlM1tqZmeb2Xozi+bL\n9Wr4WqQQanEWERGRNmVmp5FbYnwyudxjMbDoEKdsBWa6e72ZjSW3dPSU5gq6+wYz+y+gxt2/l7/f\nc8AlwEP5+/7B3dPHqDrSjanFWURERNra2cCD7l7r7nuAuYcpHwX+28zeAH4PTDjC+/2MA0tmXw/8\nzxGeL9IstTiLiIhIsWQ40IiXaLD/y0A1MCl/vP5ILuruL+W7e5wHhN192TGIVUQtziIiItLmngcu\nN7MSM+sJXJbfvwE4Lb/90Qbly4Eqdw+Aa4DwYa6/F+h50L5fAvei1mY5hpQ4i4iISJty98XA74DX\ngMeABflD3wNuNrMlQL8Gp/wEuM7MXgPGA/sOc4s/Ah95f3Bgft9vgN7k+keLHBPm7sWOQURERLoR\nM7udBoP52ugeHwVmu/s1bXUP6X7Ux1lERES6FDP7D+BDwKxixyJdi1qcRURERERaQX2cRURERERa\nQYmziIiIiEgrKHEWEREREWkFJc4iIiIiIq2gxFlEREREpBWUOIuIiIiItML/AsR5jzE5TiVwAAAA\nAElFTkSuQmCC\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1ea0194f7b8>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"colors = [\"#9b59b6\", \"#3498db\", \"#95a5a6\", \"#e74c3c\", \"#34495e\", \"#2ecc71\"]\n",
"plt.figure(figsize=(12, 4))\n",
"\n",
"plt.subplot(121)\n",
"plt.scatter(representation[:, 0], representation[:, 1], c=colors)\n",
"\n",
"plt.subplot(122)\n",
"sns.countplot(x='quality', data=data, palette=sns.color_palette(colors));"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"Moreover, our classes are highly unbalanced, so in our classifier we should add parameter class_weight='balanced'."
]
},
{
"cell_type": "code",
"execution_count": 7,
"metadata": {},
"outputs": [],
"source": [
"predictors = data.iloc[:, :11]\n",
"target = data.quality"
]
},
{
"cell_type": "code",
"execution_count": 8,
"metadata": {},
"outputs": [],
"source": [
"(predictors_train, predictors_test,\n",
" target_train, target_test) = train_test_split(predictors, target, test_size = .3, random_state = rnd_state)"
]
},
{
"cell_type": "markdown",
"metadata": {},
"source": [
"#### RandomForest classifier "
]
},
{
"cell_type": "code",
"execution_count": 9,
"metadata": {},
"outputs": [],
"source": [
"list_estimators = list(range(1, 50, 5))\n",
"rf_scoring = []\n",
"for n_estimators in list_estimators:\n",
" classifier = RandomForestClassifier(random_state = rnd_state, n_jobs = -1, \n",
" class_weight='balanced', n_estimators=n_estimators)\n",
" score = cross_val_score(classifier, predictors_train, target_train, cv=5, \n",
" n_jobs=-1, scoring = 'accuracy') \n",
" rf_scoring.append(score.mean())"
]
},
{
"cell_type": "code",
"execution_count": 10,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAAEICAYAAABYoZ8gAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VfWd//HXhyyQsIQlYV/CvooLKbhVLegMtY50cRzt\nWG07LWOnduxetfOrU1u7zHTRVi1jrVVbW6dVqlStWqLWpeoAFtkuyKYkLNkQQgIh2+f3xznBS0zM\nBZLc3Hvez8fjPnKW7znne07gfU++53zPMXdHRESio1eyKyAiIt1LwS8iEjEKfhGRiFHwi4hEjIJf\nRCRiFPwiIhGj4BeRd2Vm95jZt5NdD+k8Cv4IM7NnzewtM+ud7Lp0BTPbaGafbGP6tWa2MhyeaWZP\nmdleM9tnZqvM7MJ21vdxM3uhq+st0tUU/BFlZoXAewEHLu7mbWd206buBa5sY/rHwnkAfwT+DAwH\nhgL/DlQf7wbNLON4l40CHZ+eQcEfXVcCLwP3AFfFzzCzHDP7oZm9aWb7zewFM8sJ551tZn8Nz45L\nzOzj4fRnzexTces46uzYzNzMPmtmm4HN4bRbw3VUh2fa740rn2FmN5jZVjM7EM4fY2a3m9kPW9V3\nmZl9oY19/BVwtpmNiys7A5gN/NbM8oHxwM/dvT78vOju7zirN7PpwBLgDDOrMbN94fR7zOxnZva4\nmdUC7zOz3mb2AzPbYWZlZrak5fiFy1xkZqvDY/hXM5sdN+9rZrYz3OdNZragrV9euN3bzeyxsOwr\nZjYxnFcYHu/MuPJHfj/h7+ZFM/txWIdtZnZmOL3EzMrN7KpWm8w3sz+H2/pLq2M6LZy3N6zzpa3q\nedTxaWt/pJu5uz4R/ABbgH8D5gANwLC4ebcDzwKjgAzgTKA3MA44AFwOZAFDgFPCZZ4FPhW3jo8D\nL8SNO8GZ9WAgJ5x2RbiOTOBLwB6gTzjvK8BaYCpgwMlh2bnALqBXWC4fOBhf/1b7+WfgP+LGvws8\nHA4bwZfQo8AH21tHe/sUTrsH2A+cRXAi1Qf4MbAs3Nf+BH9VfDcsfypQDswLj+1VwBvh8Z0KlAAj\nw7KFwMR26nIPUBUej0zgfuCBuOUcyIwrf+T3E+5HI/CJsA7fBnaEv/fewN+Fv+d+cds6AJwTzr+1\n5TgAfcM6fyKsx6lAJTCjveOT7H/7+riCP4of4GyCsM8PxzcCXwiHewGHgJPbWO564A/trPNIsITj\nR4VkGETzO6jXWy3bBTYBi9opFwMuCIevAR5/l3VeAWyK27cdwIfi5o8GbgO2As3Ac8DkdtZ11D6F\n0+4B7osbN6A2PrCBM4Dt4fDPgG+1Wscm4FxgEsGXwvlAVgfH6h7grrjxC4GN4XAiwb85bt5JYfn4\nL/8q3v5Sv4fwSyUc7wc0AWOAfwKeb1W3/wFubOv46NMzPmrqiaargKfcvTIc/w1vN/fkE5y1bm1j\nuTHtTE9USfyImX3ZzGJhc9I+IC/cfkfbupcg0Al//updtrkUGGFmpwPnAbnAYy0z3b3U3a9x94kE\nf9HUAvcd014dvV8F4TZWhc0o+4AnwumE2/hSy7xw/hiCs/wtwOeB/wTKzewBMxv5LtvdEzd8kCCQ\nE1UWN3wIwN1bT4tf35F9dPcaYC8wMtyfea32558Jrpm8Y1npGbrrIpv0EGFb86VAhpm1BEdvYKCZ\nnUzQvFIHTARea7V4CUHTQltqCQKvxfA2yhx5FGzYnv9VYAGw3t2bzewtgjPmlm1NBNa1sZ5fA+vC\n+k4HHm6nTrj7QTN7kOCaRg7BmWt9O2VLzOx24LftrS6B6ZUEoTnT3Xe2UbYEuNndb26nDr8BfmNm\nAwjOnL9PcDH6WNSGP3N5+0J1W7+PYzGmZcDM+hE0Y+0i2J+/uPsF77KsHgHcw+iMP3o+SPBn+gzg\nlPAzHXgeuNLdm4G7gR+Z2cjwIusZFtzyeT9wvpldamaZZjbEzE4J17sa+LCZ5ZrZJOBfOqhHf4J2\n5gog08y+AQyIm38X8C0zm2yB2WY2BIKzdGAFwZn+Q+5+qINt3UvQJPER3r6bBzMbZGbfNLNJZtYr\nvNj7SYKL3m0pA0abWXZ7GwqP38+BH5vZ0HA7o8zs78MiPweuNrN54X71NbMPmFl/M5tqZvPDY11H\n8AXS3MG+tVWHCmAncEX4+/skwZfoibjQggv72cC3gJfdvYTg+sgUM/uYmWWFn/dYcDFceigFf/Rc\nBfzS3Xe4+56WD0E79z+Hd4J8meDMfwXBn/TfJ7iYuoOgLflL4fTVBBddIbigWU8QjvcSfEm8mycJ\nmkBeB94kCLr4JoEfAb8DniI4a/0FwRl7i3sJ2qbfrZmnxXMEFxhL3X1F3PR6gvbw5eE21gGHCdrA\n2/I0sB7YY2aV7ZQB+BrBxfOXzaw6XP9UAHdfCXya4Hi/FZZr2V5v4HsEfzXsIbi99PoE9q8tnya4\nQF4FzAT+epzrafEb4EaC3/scwqY2dz9AcDH4MoK/APYQ/HtJy74h6cLc9VeYpB4zO4egyWec6x+x\nyDHRGb+kHDPLAq4luKtFoS9yjBT8klLCtuN9wAjgliRXRyQlqalHRCRidMYvIhIxPfI+/vz8fC8s\nLEx2NUREUsaqVasq3b2g45I9NPgLCwtZuXJlsqshIpIyzOzNRMuqqUdEJGIU/CIiEaPgFxGJGAW/\niEjEKPhFRCJGwS8iEjEKfhGRiOmR9/GLiERBU7Oza98htlfWsr2ylkMNTVx97om+OqFjCn4RkS7k\n7pRVH2Z7ZS1vVNUeCfntlbXsqDpIfdPb79op6N+bfz1nAmb2Lms8cQp+EZET5O68dbCB7ZU1bK88\nyPbKGt6oPMi2ylrerKrlYH3TkbLZmb0oHJLLhPy+LJg2lPH5fSnM78uE/L4U9O/d5aEPCn4RkYRV\n1zXwRni2/kYY8NurDrK9oobqusYj5TJ6GWMG5TA+vy+nTxjMhDDcx+f3ZUReDhm9uj7c342CX0Qk\nTl1DU9AkU1HL9vBnSxNNZU39kXJmMDIvCPeLTxnJ+Px+jM/PpXBIX8YMziUro+feO6PgF5FIqj3c\nyMY91WzYVc3GPQfCs/hadu2vO6pcQf/ejB/SlwXThh05ax+f35dxQ3Lpk5WRpNqfGAW/iKS98gN1\nrN8VhPyG3dXEdlWzvaqWlvdQDeiTyYSCfpw+Ycg7wr1/n6zkVr4LKPhFJG00NTtvVNUeCfiWsK+s\nOXykzJjBOcwYMYAPnjqKGSMGMGPkAEbk9emWi6o9hYJfRFJSXUMTm/YcCMJ99/4jTTYtd9Bk9jIm\nD+vPeVMLjgT89BEDyMtJvzP4Y6XgF5Eeb29tfXgWv//IWfzWihqaw6aa/r0zmT5yAJcWjWHmyCDk\nJw3tR+/M1GyD72oKfhHpMdydkr2HWL9rPxt2v90mvzvuguuIvD7MHDmA988azoyRA5gxIo8xg3Mi\n1VRzohIKfjNbCNwKZAB3ufv32ihzHnALkAVUuvu54fSBwF3ALMCBT7r7S51SexFJWYfqm9haUfN2\nwO+qJra7mgOHg/vhexlMGtqPeeMHM2PkAGaOzGP6iAEM7pud5Jqnvg6D38wygNuBC4BSYIWZLXP3\nDXFlBgJ3AAvdfYeZDY1bxa3AE+5+iZllA7mdugci0mO5O+UHDrO1vIatFTVsrahla0UN2ypq2bnv\n0JFyOVkZTB/Rn0WnjmTmyDxmjBjA1OH9U/Z2yZ4ukTP+ucAWd98GYGYPAIuADXFlPgosdfcdAO5e\nHpbNA84BPh5OrwfqEZG0UtfQxJtVB8NQPzrgaw6/3aM1NzuDCQV9KSocxD8VjGFCQV+mjxhA4ZC+\nSe/NGiWJBP8ooCRuvBSY16rMFCDLzJ4F+gO3uvt9wHigAvilmZ0MrAKudffaE624yLF4YXMlK97Y\nixkYFv4Mel+2tA3Hz+sVNxzMs7fLt4y/Y7jVeglGWsr0smB6TlYmA3OzGJSbzcDcLPJyslLizNbd\nqaqtD8/ea8OAD4ZL3zp45EIrwMi8Pkwc2o+PnDaKiUP7MSG/HxOH9mX4gGjdNtlTddbF3UxgDrAA\nyAFeMrOXw+mnAZ9z91fM7FbgOuD/tV6BmS0GFgOMHTu2k6olUVdx4DA3PbqBP762K9lVeVc5WRlH\nvgRavhCC8WwGvWP47fldcddKQ1PzkbP3lrP2rRU1bC0/+nk0vTN7MaGgH7NH5/HBU0cxsaAvEwv6\nMaGgL7nZum+kJ0vkt7MTGBM3PjqcFq8UqArP5GvN7DngZOB5oNTdXwnLPUgQ/O/g7ncCdwIUFRV5\nW2VEEuXu/G5lCTc/FqOuoZkvnD+Fq8+bQHZGL9yDuwya3cNhP9KDM348vgytprt7+DNueltlWq23\n2eFgfSP7DjYEn0P14XD481AwvKW85shwQ1P7/x1avjAG5mYzMCfryBfC0eMtw8EXR174hfFWbT3b\nKmvYWl575Mx9W0UNb+49SFPc6fvQ/r2ZWNCPi08ZGZ6592NiQV9G5uXQS80zKSmR4F8BTDaz8QSB\nfxlBm368R4DbzCwTyCZoCvqxu+8xsxIzm+rumwj+ItiASBfaWlHDDUvX8sr2vcwtHMx3PnwSk4b2\nOzK/paUhg54fWu7Owfom9h1q4K3aevYfavsL462DDew/lPgXRnZmL+ob334OfHZGLwrzc5k6vD8X\nnjSCCXFn7+n4yIKo6zD43b3RzK4BniS4nfNud19vZleH85e4e8zMngDWAM0Et3yuC1fxOeD+8I6e\nbcAnumJHROobm1nyl63c9vQW+mT14nsfPolLi8ak9FmpmdG3dyZ9e2cyamBOwst19IWx/1ADBf16\nM3FoEPCjB+Xq4mqEmHvPa1UpKirylStXJrsakkJWvrGX65euZXN5DRfNHsE3/mEGQ/v3SXa1RLqN\nma1y96JEyuoKjKS06roGvv+njdz/yg5GDczh7o8XMX/asGRXS6RHU/BLSnJ3nli3hxuXraey5jD/\ncvZ4vnjBFPr21j9pkY7of4mknF37DvGNR9azPFbGjBEDuOuqImaPHpjsaomkDAW/pIymZufXL7/J\nfz2xkSZ3brhwGp88azyZPfgVdyI9kYJfUkJsdzXXL13L6pJ9vHdyPt/50EmMGazHPokcDwW/9Gh1\nDU38pHgzdz63jbycLG75p1NYdMpIdfsXOQEKfumxXtxSyQ1/WMubVQe5ZM5ovn7hdAbpkbwiJ0zB\nLz3O3tp6bn4sxkOvllI4JJfffGoeZ07KT3a1RNKGgl96DHfn4dU7+dajMaoPNfDZ903kc/Mnp8ST\nK0VSiYJfeoQdVQf5+sNreX5zJaeOHch3P3wS04YPSHa1RNKSgl+SqqGpmV+8sJ1blr9OZq9e3LRo\nJv88b5yeGyPShRT8kjSvlezjuqVrie2u5oIZw7hp0UxG5CX+IDIROT4Kful2tYcb+eFTr3PPX7dT\n0L83S66Yw8JZw5NdLZHIUPBLt3p6Yxn/8Yd17K6u44p54/jKwqkM0PPeRbqVgl+6RfmBOr75xw08\ntmY3U4b148GPnsGccYOTXS2RSFLwS5dqbnb+d2UJ33k8xuHGZr78d1NYfM5EsjP1fB2RZFHwS5fZ\nWlHD9Q+t5f/e2MvpEwbznQ+dxISCfh0vKCJdSsEvna6+sZn/+ctWfvr0FnKyM/ivj8zmH4tG6/k6\nIj2Egl861as73uL6h9ayqewAF80ewY3/MJOC/r2TXS0RiaPgl05Rc7iRHzy5iXtfeoPhA/rwi6uK\nWDBdr0AU6YkSCn4zWwjcCmQAd7n799oocx5wC5AFVLr7uXHzMoCVwE53v6gT6i09SPwtmleePo6v\nLJxGP70CUaTH6vB/ZxjatwMXAKXACjNb5u4b4soMBO4AFrr7DjMb2mo11wIxQA9fSSMVBw5z06Mb\n+ONru8JbNM9kzrhBya6WiHQgkdOyucAWd98GYGYPAIuADXFlPgosdfcdAO5e3jLDzEYDHwBuBr7Y\nSfWWJHJ3fr+qlJsfi3GovokvXjCFq8/VLZoiqSKR4B8FlMSNlwLzWpWZAmSZ2bNAf+BWd78vnHcL\n8NVwervMbDGwGGDs2LEJVEuS4c2qWm74w1pe3FLFewoH8d0Pz2bSUN2iKZJKOqshNhOYAywAcoCX\nzOxlgi+EcndfFV4DaJe73wncCVBUVOSdVC/pJA1Nzdz1fPAUzeyMXtz8oVlc/p6x9NJTNEVSTiLB\nvxMYEzc+OpwWrxSocvdaoNbMngNOBk4DLjazC4E+wAAz+7W7X3HiVZfusrZ0P197aA0bdlfz9zOH\n8c2LZzE8r0+yqyUixymR4F8BTDaz8QSBfxlBm368R4DbzCwTyCZoCvqxu/8euB6O3PXzZYV+6jhY\n38iPnnqdu1/cTn6/3iy54jQWzhqR7GqJyAnqMPjdvdHMrgGeJLid8253X29mV4fzl7h7zMyeANYA\nzQS3fK7ryopL13ru9Qpu+MNaSt86xEfnjeVrC6eRl6OnaIqkA3Pvec3pRUVFvnLlymRXI5L21tbz\n7Uc3sPRvO5lQ0Jfvfugk5k0YkuxqiUgHzGyVuxclUla9bAQIbtF8ZPUubnp0A9WHGvjc/El89n2T\n9KJzkTSk4BdK9h7k6w+v47nXKzhlzEC+9xG96FwknSn4I6yp2fnli9v54VOv08vgP/9hBh87o1Av\nOhdJcwr+iNqwq5rrlq5hTel+5k8byrc+OItRA/Wic5EoUPBHTF1DE7cWb+bO57YxKDeLn15+KhfN\nHqFn5YtEiII/Qv66tZIblq7ljaqD/OOc0Xz9A9MZmJud7GqJSDdT8EfA/oMN3Pz4Bn63spRxQ3K5\n/1PzOGtSfrKrJSJJouBPY+7OY2t385/LNvDWwXquPnci1y6YTE62btEUiTIFf5qqrDnMdQ+tYXms\nnJNG5XHPJ97DrFF5ya6WiPQACv40tH7Xfj5970qqauv5+oXT+cRZhWRm6Fn5IhJQ8KeZx9bs5su/\nf42BuVk89JkzdZYvIu+g4E8Tzc3OLcWb+UnxZuaMG8SSK+ZQ0L93sqslIj2Qgj8N1B5u5Iu/W82T\n68v4xzmj+faHZtE7UxdwRaRtCv4UV7L3IJ++byWvlx3g/100g0+eVajOWCLyrhT8KezlbVX82/2v\n0tjUzD2fmMs5UwqSXSURSQEK/hR1/ytvcuMj6xk7JJe7rixiQoFeeC4iiVHwp5iGpmZu+uMGfvXy\nm5w3tYCfXH4qA/rozVgikjgFfwrZW1vPv92/ipe37eVfz5nAVxdO0yOUReSYKfhTxKY9B/jUfSso\nqz7Mjy49mQ+fNjrZVRKRFJVQd04zW2hmm8xsi5ld106Z88xstZmtN7O/hNPGmNkzZrYhnH5tZ1Y+\nKv68oYwP3/Eihxua+d/Fpyv0ReSEdHjGb2YZwO3ABUApsMLMlrn7hrgyA4E7gIXuvsPMhoazGoEv\nufurZtYfWGVmf45fVtrn7tzx7FZ+8NQmThqVx50fK2J4Xp9kV0tEUlwiTT1zgS3uvg3AzB4AFgHx\n4f1RYKm77wBw9/Lw525gdzh8wMxiwKhWy0obDtU38ZUHX+PRNbtZdMpIvv+R2XrxuYh0ikSCfxRQ\nEjdeCsxrVWYKkGVmzwL9gVvd/b74AmZWCJwKvNLWRsxsMbAYYOzYsQlUK33t2neIxb9ayfpd1Xxt\n4TSuPneCOmWJSKfprIu7mcAcYAGQA7xkZi+7++sAZtYPeAj4vLtXt7UCd78TuBOgqKjIO6leKWfV\nm2/xr79aRV1DE3ddWcSC6cOSXSURSTOJBP9OYEzc+OhwWrxSoMrda4FaM3sOOBl43cyyCEL/fndf\n2gl1Tlu/X1nC1/+wjhED+/DbT89j8rD+ya6SiKShRO7qWQFMNrPxZpYNXAYsa1XmEeBsM8s0s1yC\npqCYBe0TvwBi7v6jzqx4OmlsauZbj27gKw+u4T3jB/HIZ89S6ItIl+nwjN/dG83sGuBJIAO4293X\nm9nV4fwl7h4zsyeANUAzcJe7rzOzs4GPAWvNbHW4yhvc/fEu2ZsUtP9gA9f89lWe31zJx88s5Osf\nmE6WXpoiIl3I3Htec3pRUZGvXLky2dXoclsravj0vSspeesgNy2axeVzo31RW0SOn5mtcveiRMqq\n526SPLOpnH//7d/IzujF/Z86nbnjBye7SiISEQr+bubu3PX8dr77pxhThw/g51fOYfSg3GRXS0Qi\nRMHfjeoamrjhD2tZ+upO3j9rOD+89GRys/UrEJHupdTpJuXVdSz+1SpWl+zjC+dP4XPzJ9FLT9YU\nkSRQ8HeDNaX7WHzfKvYfamDJFaexcNaIZFdJRCJMwd/FHlm9k68+uIb8fr156DNnMmPkgGRXSUQi\nTsHfRZqbnR88tYk7nt3K3MLB/OyK0xjSr3eyqyUiouDvCgfqGvjC/65meaycy+eO4ZsXzyI7U52y\nRKRnUPB3skP1TVzys5fYUlHDTYtm8rHTx+nJmiLSoyj4O9mzm8rZVHaA2z96Gh+YrYu4ItLzqP2h\nky2PlZOXk8Xfz9TjlEWkZ1Lwd6KmZufZTeWcN7WATD1oTUR6KKVTJ1pdso+q2nrmTxvacWERkSRR\n8Hei4lgZGb2M86Yo+EWk51Lwd6KnN5bznsJB5OVmJbsqIiLtUvB3ktK3DrJxzwEWTNNFXRHp2RT8\nnaQ4Vg7Agulq5hGRnk3B30mKN5YzIb8vEwr6JbsqIiLvSsHfCWoON/Ly1irdzSMiKSGh4DezhWa2\nycy2mNl17ZQ5z8xWm9l6M/vLsSyb6l7YXEF9UzMLpqt9X0R6vg4f2WBmGcDtwAVAKbDCzJa5+4a4\nMgOBO4CF7r7DzIYmumw6KI6VM6BPJkWFg5JdFRGRDiVyxj8X2OLu29y9HngAWNSqzEeBpe6+A8Dd\ny49h2ZTW3Ow8s6mcc6cOJUu9dUUkBSSSVKOAkrjx0nBavCnAIDN71sxWmdmVx7BsSltduo/KmnrO\n1908IpIiOuvpnJnAHGABkAO8ZGYvH8sKzGwxsBhg7NixnVStrvd0rJyMXsa5UwqSXRURkYQkcsa/\nExgTNz46nBavFHjS3WvdvRJ4Djg5wWUBcPc73b3I3YsKClInRJfHypgzbhADc7OTXRURkYQkEvwr\ngMlmNt7MsoHLgGWtyjwCnG1mmWaWC8wDYgkum7JaeuuqmUdEUkmHTT3u3mhm1wBPAhnA3e6+3syu\nDucvcfeYmT0BrAGagbvcfR1AW8t20b50u2c2tvTW1W2cIpI6Emrjd/fHgcdbTVvSavy/gf9OZNl0\nsTxWTuGQXCbk9012VUREEqb7D49T7eFGXtpaxYLpw/ROXRFJKQr+4/TClsqwt67a90UktSj4j1Nx\nrIz+fTJ5T+HgZFdFROSYKPiPQ3Oz8/TGCs6dUqDeuiKScpRax2HNzv1U1hzmfN3NIyIpSMF/HIpj\nZfQy1FtXRFKSgv84LI+VUzRuMIP6qreuiKQeBf8x2rXvELHd1bqbR0RSloL/GBVv1Lt1RSS1KfiP\nUXGsjHFDcpmod+uKSIpS8B+Dg/WN/HVrFQumqbeuiKQuBf8xeGFzJfWN6q0rIqlNwX8MimPl9O+t\n3roiktoU/AlqbnaKN5ZzztQCsjN12EQkdSnBErQ27K27YJqaeUQktSn4E9TSW/d9UxX8IpLaFPwJ\nWh4rZ864QeqtKyIpT8GfgN37D7FhdzXzp+mhbCKS+hT8CSiOBb119VJ1EUkHCv4EFMfKGDs4l0lD\n1VtXRFJfQsFvZgvNbJOZbTGz69qYf56Z7Tez1eHnG3HzvmBm681snZn91sz6dOYOdLWD9Y28uLWK\n+dOGqreuiKSFDoPfzDKA24H3AzOAy81sRhtFn3f3U8LPTeGyo4B/B4rcfRaQAVzWabXvBi9uqaK+\nsVkvXRGRtJHIGf9cYIu7b3P3euABYNExbCMTyDGzTCAX2HXs1Uye4lgZ/XpnMne8euuKSHpIJPhH\nASVx46XhtNbONLM1ZvYnM5sJ4O47gR8AO4DdwH53f6qtjZjZYjNbaWYrKyoqjmknukrwbt1yzpmS\nr966IpI2OivNXgXGuvts4KfAwwBmNojgr4PxwEigr5ld0dYK3P1Ody9y96KCgp7xSsN1u/ZTfuAw\nC3Qbp4ikkUSCfycwJm58dDjtCHevdveacPhxIMvM8oHzge3uXuHuDcBS4MxOqXk3WB4rD3rr6jEN\nIpJGEgn+FcBkMxtvZtkEF2eXxRcws+EW3vJiZnPD9VYRNPGcbma54fwFQKwzd6ArPb2xjNPGDmKw\neuuKSBrpMPjdvRG4BniSILR/5+7rzexqM7s6LHYJsM7MXgN+AlzmgVeABwmagtaG27uzC/aj0+3Z\nX8e6ndXMV6ctEUkzmYkUCptvHm81bUnc8G3Abe0seyNw4wnUMSmKN5YB6DZOEUk7ulWlHU/Hyhkz\nOIfJ6q0rImlGwd+GQ/VNvLClUu/WFZG0pOBvw4tbKjmsd+uKSJpS8LeheGM5fbMzmDd+SLKrIiLS\n6RT8rbg7T28s45wpereuiKQnJVsr63ZWU1Z9mAW6m0dE0pSCv5XijWWYwfum9ozHRoiIdDYFfyvF\nsXJOHTOQIf16J7sqIiJdQsEfp6y6jrU796uZR0TSmoI/ztMbW96tq+AXkfSl4I9THCtj1MAcpgxT\nb10RSV8K/lBdQ9Bb9/zpereuiKQ3BX/or1srqWtoVvu+iKQ9BX9oeSzsrTtB79YVkfSm4CfsrRsr\n572TC+idmZHs6oiIdCkFP7B+VzV7quv0UDYRiQQFP0GnLdO7dUUkIhT8BI9pOGXMQPLVW1dEIiDy\nwV9eXcea0v3qtCUikZFQ8JvZQjPbZGZbzOy6NuafZ2b7zWx1+PlG3LyBZvagmW00s5iZndGZO3Ci\nWnrrzlczj4hERIcvWzezDOB24AKgFFhhZsvcfUOros+7+0VtrOJW4Al3v8TMsoHcE610Z1oeK2fU\nwBymDe+f7KqIiHSLRM745wJb3H2bu9cDDwCLElm5meUB5wC/AHD3enffd7yV7Wx1DU28uKWSBeqt\nKyIRkkjwjwJK4sZLw2mtnWlma8zsT2Y2M5w2HqgAfmlmfzOzu8ysb1sbMbPFZrbSzFZWVFQcyz4c\nt5e2VnFTaOUCAAAIBklEQVSooUnNPCISKZ11cfdVYKy7zwZ+CjwcTs8ETgN+5u6nArXAO64RALj7\nne5e5O5FBQXd8xKU5bEycrMzOH2C3q0rItGRSPDvBMbEjY8Opx3h7tXuXhMOPw5kmVk+wV8Hpe7+\nSlj0QYIvgqQL3q1bznsn59MnS711RSQ6Egn+FcBkMxsfXpy9DFgWX8DMhlvYSG5mc8P1Vrn7HqDE\nzKaGRRcArS8KJ8WG3dXs3l/Hgmm6jVNEoqXDu3rcvdHMrgGeBDKAu919vZldHc5fAlwCfMbMGoFD\nwGXu7uEqPgfcH35pbAM+0QX7cczUW1dEoqrD4IcjzTePt5q2JG74NuC2dpZdDRSdQB27RHGsjJNH\nD6Sgv3rriki0RLLnbvmBOl4r3c8Cne2LSARFMvifCXvr6qUrIhJFkQz+5bFyRub1YfoI9dYVkeiJ\nXPDXNTTxwuZK5qu3rohEVOSC/6VtQW9dNfOISFRFLviLY2XkZGVwhnrrikhERSr4W96te7Z664pI\nhEUq+GO7D7Brfx3n6926IhJhkQr+4lgZoN66IhJt0Qr+jeWcPDqPof37JLsqIiJJE5ngrzhwmNdK\n9+luHhGJvMgE/zMby3GHBWrfF5GIi0zwF28sY0ReH2aMGJDsqoiIJFUkgr+uoYnnN1cyf5p664qI\nRCL4X95WxcH6Js5X+76ISDSC/+mN5fTJ6sUZE9VbV0Qk7YPf3SmOlXP2pAL11hURIQLBv3HPAXbu\nO6TeuiIiobQP/qfDl67MV29dEREgweA3s4VmtsnMtpjZdW3MP8/M9pvZ6vDzjVbzM8zsb2b2aGdV\nPFHLY2XMHp3H0AHqrSsiAgm8bN3MMoDbgQuAUmCFmS1z9w2tij7v7he1s5prgRjQrTfRV9YcZnXJ\nPj6/YEp3blZEpEdL5Ix/LrDF3be5ez3wALAo0Q2Y2WjgA8Bdx1fF46feuiIi75RI8I8CSuLGS8Np\nrZ1pZmvM7E9mNjNu+i3AV4Hm46/m8SmOlTN8QB9mjlRvXRGRFp11cfdVYKy7zwZ+CjwMYGYXAeXu\nvqqjFZjZYjNbaWYrKyoqTrhChxubeH5zhd6tKyLSSiLBvxMYEzc+Opx2hLtXu3tNOPw4kGVm+cBZ\nwMVm9gZBE9F8M/t1Wxtx9zvdvcjdiwoKCo59T1p5ZdteauubWKC7eUREjpJI8K8AJpvZeDPLBi4D\nlsUXMLPhFp5Wm9nccL1V7n69u49298Jwuafd/YpO3YN2FMfK6JPVi7Mm5XfH5kREUkaHd/W4e6OZ\nXQM8CWQAd7v7ejO7Opy/BLgE+IyZNQKHgMvc3buw3h3VmeWxcs6epHfrioi01mHww5Hmm8dbTVsS\nN3wbcFsH63gWePaYa3gcXi+rYee+Q3z2fZO6Y3MiIiklLXvuLg/fravbOEVE3iktg784VsZJo/IY\npt66IiLvkHbBX1VzmL+V7NPZvohIO9Iu+J/ZVBH01p2ml66IiLQl7YK/OFbGsAG9mTVKvXVFRNqS\nVsFf39jMc69XMH/aMPXWFRFpR1oF/yvbq9RbV0SkA2kV/MWxcnpnqreuiMi7SZvgd3eKN5Zx9qR8\ncrLVW1dEpD0J9dxNBXUNzZw5IZ8zJw1JdlVERHq0tAn+nOwMvn/J7GRXQ0Skx0ubph4REUmMgl9E\nJGIU/CIiEaPgFxGJGAW/iEjEKPhFRCJGwS8iEjEKfhGRiLEkvhO9XWZWAbz5LkXygcpuqk4q0PF4\nm47F0XQ8jpbOx2OcuxckUrBHBn9HzGyluxclux49hY7H23QsjqbjcTQdj4CaekREIkbBLyISMaka\n/HcmuwI9jI7H23QsjqbjcTQdD1K0jV9ERI5fqp7xi4jIcVLwi4hETEoFv5ktNLNNZrbFzK5Ldn26\nm5ndbWblZrYubtpgM/uzmW0Ofw5KZh27k5mNMbNnzGyDma03s2vD6ZE7JmbWx8z+z8xeC4/FN8Pp\nkTsW8cwsw8z+ZmaPhuORPh4tUib4zSwDuB14PzADuNzMZiS3Vt3uHmBhq2nXAcXuPhkoDsejohH4\nkrvPAE4HPhv+m4jiMTkMzHf3k4FTgIVmdjrRPBbxrgViceNRPx5ACgU/MBfY4u7b3L0eeABYlOQ6\ndSt3fw7Y22ryIuDecPhe4IPdWqkkcvfd7v5qOHyA4D/4KCJ4TDxQE45mhR8ngseihZmNBj4A3BU3\nObLHI14qBf8ooCRuvDScFnXD3H13OLwHGJbMyiSLmRUCpwKvENFjEjZrrAbKgT+7e2SPRegW4KtA\nc9y0KB+PI1Ip+KUDHtybG7n7c82sH/AQ8Hl3r46fF6Vj4u5N7n4KMBqYa2azWs2PzLEws4uAcndf\n1V6ZKB2P1lIp+HcCY+LGR4fToq7MzEYAhD/Lk1yfbmVmWQShf7+7Lw0nR/qYuPs+4BmC60FRPRZn\nAReb2RsEzcLzzezXRPd4HCWVgn8FMNnMxptZNnAZsCzJdeoJlgFXhcNXAY8ksS7dyswM+AUQc/cf\nxc2K3DExswIzGxgO5wAXABuJ4LEAcPfr3X20uxcSZMXT7n4FET0eraVUz10zu5Cg3S4DuNvdb05y\nlbqVmf0WOI/g0bJlwI3Aw8DvgLEEj7K+1N1bXwBOS2Z2NvA8sJa323FvIGjnj9QxMbPZBBcrMwhO\n6H7n7jeZ2RAidixaM7PzgC+7+0U6HoGUCn4RETlxqdTUIyIinUDBLyISMQp+EZGIUfCLiESMgl9E\nJGIU/CIiEaPgFxGJmP8PFpx2DW1pR/4AAAAASUVORK5CYII=\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1ea01939978>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.plot(list_estimators, rf_scoring)\n",
"plt.title('Accuracy VS trees number');"
]
},
{
"cell_type": "code",
"execution_count": 11,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"RandomForestClassifier(bootstrap=True, class_weight='balanced',\n",
" criterion='gini', max_depth=None, max_features='auto',\n",
" max_leaf_nodes=None, min_impurity_decrease=0.0,\n",
" min_impurity_split=None, min_samples_leaf=1,\n",
" min_samples_split=2, min_weight_fraction_leaf=0.0,\n",
" n_estimators=20, n_jobs=-1, oob_score=False, random_state=4536,\n",
" verbose=0, warm_start=False)"
]
},
"execution_count": 11,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"classifier = RandomForestClassifier(random_state = rnd_state, n_jobs = -1, \n",
" class_weight='balanced', n_estimators=20)\n",
"classifier.fit(predictors_train, target_train)"
]
},
{
"cell_type": "code",
"execution_count": 12,
"metadata": {},
"outputs": [],
"source": [
"prediction = classifier.predict(predictors_test)"
]
},
{
"cell_type": "code",
"execution_count": 13,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Confusion matrix:\n",
" Predicted 3 4 5 6 7 All\n",
"Actual \n",
"3 0 0 3 0 0 3\n",
"4 0 1 9 6 0 16\n",
"5 2 1 166 41 3 213\n",
"6 0 0 46 131 14 191\n",
"7 0 0 5 25 23 53\n",
"8 0 0 0 3 1 4\n",
"All 2 2 229 206 41 480\n",
"\n",
"Accuracy: 0.66875\n"
]
}
],
"source": [
"print('Confusion matrix:\\n', pd.crosstab(target_test, prediction, colnames=['Predicted'], \n",
" rownames=['Actual'], margins=True))\n",
"print('\\nAccuracy: ', accuracy_score(target_test, prediction))"
]
},
{
"cell_type": "code",
"execution_count": 14,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"volatile acidity 0.133023\n",
"alcohol 0.130114\n",
"sulphates 0.129498\n",
"citric acid 0.106427\n",
"total sulfur dioxide 0.094647\n",
"chlorides 0.086298\n",
"density 0.079843\n",
"pH 0.066566\n",
"residual sugar 0.061344\n",
"fixed acidity 0.058251\n",
"free sulfur dioxide 0.053990\n",
"dtype: float64"
]
},
"execution_count": 14,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"feature_importance = pd.Series(classifier.feature_importances_, \n",
" index=data.columns.values[:11]).sort_values(ascending=False)\n",
"feature_importance"
]
},
{
"cell_type": "code",
"execution_count": 15,
"metadata": {},
"outputs": [],
"source": [
"et_scoring = []\n",
"for n_estimators in list_estimators:\n",
" classifier = ExtraTreesClassifier(random_state = rnd_state, n_jobs = -1, \n",
" class_weight='balanced', n_estimators=n_estimators)\n",
" score = cross_val_score(classifier, predictors_train, target_train, cv=5, \n",
" n_jobs=-1, scoring = 'accuracy') \n",
" et_scoring.append(score.mean())"
]
},
{
"cell_type": "code",
"execution_count": 16,
"metadata": {},
"outputs": [
{
"data": {
"image/png": "iVBORw0KGgoAAAANSUhEUgAAAX4AAAEICAYAAABYoZ8gAAAABHNCSVQICAgIfAhkiAAAAAlwSFlz\nAAALEgAACxIB0t1+/AAAIABJREFUeJzt3Xl8VPd57/HPgzYkgSRAYpGQAGPwwo4JEMfJpbFpSOLE\nbuKmju3E2Uzdxo2TJk2c3rZp2uZ2SZvlNk58Xduxk2DT1HFtkrh2nDheshiDBDab2a3RAkjASAKx\naHvuH3OEB0WgAUYazZzv+/XSi5lzzpzznJ/E95z5nc3cHRERCY8RqS5ARESGloJfRCRkFPwiIiGj\n4BcRCRkFv4hIyCj4RURCRsEvImdlZg+a2T+kug5JHgV/iJnZc2YWNbO8VNcyGMzsNTP7WD/D7zSz\n9cHrWWb2MzM7bGYtZlZtZu86w/w+Yma/Guy6RQabgj+kzGwq8FbAgfcO8bKzh2hRDwEf7mf4h4Jx\nAD8GngEmAuOBTwFt57tAM8s638+GgdpneFDwh9eHgZeAB4Fb40eYWb6Z/ZuZ1ZpZq5n9yszyg3FX\nmdlvgr3jOjP7SDD8OTP7RNw8Tts7NjM3s0+a2U5gZzDsm8E82oI97bfGTZ9lZn9pZrvN7EgwvtLM\n7jazf+tT7xoz+0w/6/h94CozmxI37eXAXOARMysFpgH/4e4dwc+v3f139urN7DLgHuDNZnbUzFqC\n4Q+a2XfM7Ekzawd+z8zyzOxfzSxiZgfM7J7e9gs+c62ZbQza8DdmNjdu3BfMrCFY5+1mdnV/v7xg\nuXeb2U+Dadea2fRg3NSgvbPjpj/1+wl+N782s68HNewxsyuD4XVm1mRmt/ZZZKmZPRMs6/k+bXpp\nMO5wUPMH+tR5Wvv0tz4yxNxdPyH8AXYBfwpcAXQCE+LG3Q08B1QAWcCVQB4wBTgCfBDIAcYB84PP\nPAd8Im4eHwF+Fffeie1ZjwXyg2G3BPPIBj4L7AdGBuP+AtgEXAIYMC+YdjHQCIwIpisFjsXX32c9\nnwH+Ku79PwKPB6+N2EboJ8D1Z5rHmdYpGPYg0Aq8hdiO1Ejg68CaYF1HE/tW8Y/B9AuAJmBJ0La3\nAq8H7XsJUAeUB9NOBaafoZYHgUNBe2QDq4DVcZ9zIDtu+lO/n2A9uoCPBjX8AxAJfu95wO8Hv+dR\nccs6ArwtGP/N3nYACoOaPxrUsQA4CFx+pvZJ9d++flzBH8Yf4CpiYV8avH8N+EzwegRwHJjXz+e+\nCPz3GeZ5KliC96eFZBBEbx+grmjvcoHtwHVnmG4bsDx4fQfw5FnmeQuwPW7dIsAfxI2fDHwL2A30\nAC8AM84wr9PWKRj2IPC9uPcGtMcHNvBmYG/w+jvA3/eZx3bgfwEXE9soXAPkDNBWDwL3xb1/F/Ba\n8DqR4N8ZN25OMH38xv8Qb2zUHyTYqATvRwHdQCXwR8CLfWr7f8CX+msf/QyPH3X1hNOtwM/c/WDw\n/mHe6O4pJbbXurufz1WeYXii6uLfmNnnzGxb0J3UAhQHyx9oWQ8RC3SCf79/lmU+Bkwys6XAMqAA\n+GnvSHevd/c73H06sW807cD3zmmtTl+vsmAZ1UE3SgvwVDCcYBmf7R0XjK8ktpe/C/g08LdAk5mt\nNrPysyx3f9zrY8QCOVEH4l4fB3D3vsPi53dqHd39KHAYKA/WZ0mf9bmZ2DGT3/msDA9DdZBNhomg\nr/kDQJaZ9QZHHlBiZvOIda+cAKYDr/T5eB2xroX+tBMLvF4T+5nm1K1gg/78zwNXA1vcvcfMosT2\nmHuXNR3Y3M98fgBsDuq9DHj8DDXh7sfM7FFixzTyie25dpxh2jozuxt45EyzS2D4QWKhOcvdG/qZ\ntg74irt/5Qw1PAw8bGZFxPac/5nYwehz0R78W8AbB6r7+32ci8reF2Y2ilg3ViOx9Xne3Zef5bO6\nBfAwoz3+8Lme2Nf0y4H5wc9lwIvAh929B3gA+JqZlQcHWd9ssVM+VwHXmNkHzCzbzMaZ2fxgvhuB\n95lZgZldDHx8gDpGE+tnbgayzexvgKK48fcBf29mMyxmrpmNg9heOrCO2J7+j9z9+ADLeohYl8T7\neeNsHsxsjJl92cwuNrMRwcHejxE76N2fA8BkM8s904KC9vsP4OtmNj5YToWZvSOY5D+A281sSbBe\nhWb2bjMbbWaXmNnbg7Y+QWwD0jPAuvVXQzPQANwS/P4+RmwjeiHeZbED+7nA3wMvuXsdseMjM83s\nQ2aWE/y8yWIHw2WYUvCHz63Ad9094u77e3+I9XPfHJwJ8jlie/7riH2l/2diB1MjxPqSPxsM30js\noCvEDmh2EAvHh4htJM7maWJdIDuAWmJBF98l8DXgh8DPiO213k9sj73XQ8T6ps/WzdPrBWIHGOvd\nfV3c8A5i/eE/D5axGThJrA+8P88CW4D9ZnbwDNMAfIHYwfOXzKwtmP8lAO6+HriNWHtHg+l6l5cH\n/BOxbw37iZ1e+sUE1q8/txE7QH4ImAX85jzn0+th4EvEfu9XEHS1ufsRYgeDbyT2DWA/sb+XjLw2\nJFOYu76FSfoxs7cR6/KZ4vojFjkn2uOXtGNmOcCdxM5qUeiLnCMFv6SVoO+4BZgEfCPF5YikJXX1\niIiEjPb4RURCZliex19aWupTp05NdRkiImmjurr6oLuXDTzlMA3+qVOnsn79+lSXISKSNsysNtFp\n1dUjIhIyCn4RkZBR8IuIhIyCX0QkZBIKfjNbETxZZ5eZ3XWGaZZZ7KlCW8zs+bjhJWb2qMWef7rN\nzN6crOJFROTcDXhWj8WekXk3sByoB9aZ2Rp33xo3TQnwbWCFu0d670oY+CbwlLvfENzZL/7WvSIi\nMsQS2eNfDOxy9z3BfcxXA9f1meYm4LHg7o24exOAmRUTe1zb/cHwDndvSVbxIiJy7hIJ/gpOv11u\nfTAs3kxgTPBA52oz+3AwfBqx+61/18w2mNl9ZlbY30LMbKWZrTez9c3Nzee4GiKSbnY1HeG+F/ew\nsa4F3TpmaCXrAq5sYvfovprYPdN/a2YvBcMXAn/m7mvN7JvAXcBf952Bu98L3AuwaNEi/RWIZKCT\nXd08tXk/D6+NsHbv4VPDp5UWct38cq6fX8HU0n73DSWJEgn+BuIeu0bs4dR9HylXDxxy93ag3cxe\nIPaAjheJPfxibTDdo8SCX0RCpPZQOw+/HOG/1tdzuL2DyrH5fGHFpayYPZG1ew7x+MYGvvmLnXzj\n5zuZV1nC9fPLuXZuOWWj9TyXwZBI8K8DZpjZNGKBfyOxPv14TwDfCp7elAssAb7u7vvNrM7MLnH3\n7cS+EWxFRDJeZ3cPv9h2gFVrI7y48yBZI4xrLhvPTUum8NaLSxkxIvZ45Wmlhdy4uIp9rcdZs7GR\nxzc28uUfb+UffrqNt1xcyh8sKOf3L59IYd6wvMNMWkrotsxm9i5i9z7PAh5w96+Y2e0A7n5PMM1f\nAB8l9ozQ+9z9G8Hw+cSen5oL7AE+6u7Rsy1v0aJFrnv1iKSnhpbj/OfLEVavq6PpyEkmFY/kxjdV\n8UdvqmRi8ciE5rF9/xEe39jAmo2NNLQcJz8ni+WXT+D6BeW8dUYZOVm6BKkvM6t290UJTTscD6oo\n+EXSS3eP8/yOJla9FOGX25twYNnMMm5eMoVll5SRfZ5B3dPjrK+N8vjGBp7ctI+WY52MLczl3XMm\ncf2CchZWjcHMkrsyaUrBLyJDoqntBP+5ro7V6+poaDlO6ag8/uhNk7nxTVVUjk3uJTsdXT08v6OZ\nxzc28POtBzjZ1UPl2Hyum1fB9QvKuXj86KQuL90o+EVk0PT0OL/ZfYhVa2t5ZusBunqct1w8jpuX\nTGH55ROGpBvmyIlOnt5ygCc2NvDrXQfpcZhdUcT18yt4z7xyJhQl1qWUSRT8IpJ0h46e5NHqeh5+\nOULtoWOMKcjhDxdV8sHFVUxL4SmYTW0nWPNKI09sbGRTQytmcOX0cVw3v4IVsydSNDInZbUNJQW/\nSJymthN8+cdbWbv3UKpLAWBcYR7TSgu5qKyQi8pGMa20kOllhZQU5Ka6tN/h7ry89zCr1kZ4avN+\nOrp7WDx1LDctqWLF7ImMzMlKdYmn2dV0lDUbG3h8YyORw8fIzR7B8ssmcN38cpZdMp7c7Mw9KKzg\nFyEWWo9W1/P3P9nKya4e3jOvnLwU/8d3oKntJHsOHiVy6BhdPW/8/xtbmBvbIJSevkGoGldAXvbQ\nBmzrsU4e21DPqrURdjUdZfTIbN6/cDI3Lali5oTh35fu7tREWnhiYwM/eXUfh9s7KM7P4V1zJnH9\n/HLeNHXsqdNJM4WCX0KvoeU4X3xsEy/saGbx1LH80/vncFHZqFSXdZqu7h7qosfZ03yUvQfb2d3c\nfup105GTp6YbYTB5TAEXlRUG3xRGMb20kGllhUwsGpm0s1rcnY11LaxaG+EnrzZyorOHeZUl3Ly4\nimvnTaIgNz3Po+/s7uFXOw/y+MYGfrblAMc7u6koyec988q5fkE5l04sSnWJSaHgl9Dq6XFWvRzh\nn57chgN3vfNSblkyJe327o6c6GTvwfbf2SDsPdjOsY7uU9MV5GYxrTRugxBsHKaVFjI6wb7toye7\neHxDAw+vjbB1XxsFuVlcN7+Cm5dUMbuieLBWMSXaT3bxzNYDPL6xgRd3HqS7x7l04miunTuJhVVj\nmFVRTHF+eh4TUPBLKL1+sJ0v/OhV1u49zFUXl/KP75uT9FMKU83d2d92gr3N7ew+GNsg7GmObRDq\no8eI6zmibHTeqW6ji+KOKVSOySc7awRbGltZtTbCExsaaO/o5rJJRdy8pIrr5pcnvNFIZwePnuSn\nr+7jvzc0sLHujZsGV40tYE5FMbMqiphTUczs8mLGFA6/4y99KfiFX2w7wFef3s4NV0zm5iVTyM8d\nXgfhkqm7x/nur/fyrz/bTk7WCP7q3ZfxgUWVobuw52RXN7WHjrGnuZ09B9/YIOxpPkr0WOep6bJH\nGGWj89jXeoK87BG8Z145Ny2pYkFlSejarNfh9g42N7SyqaGVzQ2tbG5spe7w8VPjK0rymVNRzJzJ\nxcwqj20Qxo0aXvcRUvCH3C+2HeD2H1RTmJdNy7FOykbn8afLpvPBxVXD7iyMC7XzwBE+/6NX2RBp\n4epLx/OVP5iT8G0BwiTa3sGe3m8IB9upO3yMhVVjeP/CyRQXZP7e/floOdbBlsY2NgUbhC0Nrbx+\n6Nip8eXFI5lVURzbIATfEMaPTt3fnoI/xJ597QC3f7+GSyeN5vsfX8Jr+9r42jM7WLv3MBOLRvLJ\n35vOB95UOeRniSRbZ3cP976wh2/+fCeFeVn87Xtn8d555aHdY5Wh0Xq8ky2NrWxpaDv17WDPwfZT\n4ycU5TG7vJjZwcZgdkUxE4ryhuTvUsEfUr98rYk//n41l0wczQ8+vuS0Pbnf7D7I15/ZwbrXo5QX\nj+STb7+YP7yiMi3Pa97S2Mpf/NerbN3XxrvnTuLL751F6TD72i3hceREJ1uDbwa93xB2Nx+lN1pL\nR+Uxp6KI2cGGYHZFMeXFyTsbq5eCP4R+ub2JP/5eNTMnjmLVx5f2+/Xd3fnVroN87ZkdbIi0UFGS\nz6euvpj3LZycFnc7PNnVzbee3cV3nttNSUEu/3D9LFbMnpTqskR+R/vJLrbt6/1W0MbmhlZ2Nh05\ndfB9bGFubCMQHC+YXVHM5DH5F7QxUPCHzHPbm1j5/WpmjB/Fqk8sGfAKUHfnuR3NfOOZHbxS30rV\n2AI+dfUMrp9fft53URxsGyJRPv/oq+xsOsr7FlbwN9dePiyvdBU5k+Md3WzbH9sIbKpvZXNjGzsP\nHDl1EV9JQQ7zK0v47kfedF4bAAV/iDy/o5nbvreei8tG8fBtA4d+PHfn2dea+NozO9jS2Ma00kLu\nvHoG75lXTtYwOe/9eEc3X3tmO/f/ai8Tikbyf943h9+7ZHyqyxJJihOd3Wzff+TU8YL2jm7+/YML\nzmteCv6QeGFHM58IQn/VJ5ac97nG7s7Pth7g68/s4LX9R5heVsid18zk2jmTUnrh09o9h/jCj17l\n9UPHuGlJFV9856WhOL9c5Hwo+EPgxZ3NfOKh9VxUNoqHLyD04/X0OE9v2c/Xf76DHQeOMnPCKD59\nzUxWzJo4pBuAoye7+JenXuN7v62lamwB//T+OVw5vXTIli+SjhT8Ge5XOw/y8YfWMa20kIdvW8rY\nJF9V2NPj/HTTPr7x8x3sbm7n0omj+fQ1M3nHrAmDflraizubuetHm2hsPc5Hr5zG594xM23vESMy\nlBT8GezXuw7ysQcHL/Tjdfc4P3m1kW/8fCd7D7Yzq7yIz1wzk6svG5/0DUDr8U6+8tOt/HB9PReV\nFfLVG+ZyxZSxSV2GSCZT8Geo3+w6yMceWseUsYU8fNuSIbtkvKu7hyc2NvLNX+wkcvgYcycX85nl\nM1k2sywpG4Bnth7gf//3Jg61d7DybRdx59UzMu4KY5HBpuDPQL/ZHdvTrxpbwMO3LU3JBUud3T38\nd00D//fZndRHj7OgqoTPXDOTt84oPa8NwOH2Dv52zRbWvNLIpRNH89Ub5jFncmbdDVJkqCj4M8xv\ndx/iow++TOWYAh5ZmZrQj9fR1cOj1fV869mdNLaeYNGUMfz58pm8efq4hDYA7rFjCF96YgttJzq5\n4/dm8CfLpqflVcQiw4WCP4O8tOcQH/3uOiaPyefh25ZSNnr43JrgZFc3P1xfz93P7mJ/2wmWTBvL\nZ5bPZOlF4874maa2E/z1E5t5essB5k4u5l9umJsxD8IQSSUFf4ZYu+cQH/nuOirG5PPIMAv9eCc6\nu1n9coRvP7ebpiMnuXL6OP58+UwWTX3j4Ky786OaBv7ux1s40dXDny+fySeumjZsrxQWSTcK/gzw\n8t7DfOS7LzOpeCSPrFya0tu9JupEZzer1kb4znO7OHi0g7fOKOUzy2cyoWgkf/nYJp7f0cyiKWP4\n5xvmMn2YPQZRJN0p+NPcutcPc+sDLzOxeCSrb1vK+KLhH/rxjnV08YOXarnn+T0cbu8gN3sE2SOM\nL6y4lA8tTb/HIIqkg3MJfl0ZM8ysf/0wH3ngZSYWpWfoAxTkZrPybdO5eckUHvrt69QePMYdb784\n4x6DKJKuFPzDSHVtbE9/QlHQvZOGoR+vMC+bP112carLEJE+dGRtmKiujXLrA+sYH4T+hDQPfREZ\nvhIKfjNbYWbbzWyXmd11hmmWmdlGM9tiZs/3GZdlZhvM7CfJKDrT1ESi3PrAy5SOyuWR2xT6IjK4\nBuzqMbMs4G5gOVAPrDOzNe6+NW6aEuDbwAp3j5hZ3xum3wlsA3TCdh8bIlFuvf9lxo3K5ZGVS/Wg\ncBEZdIns8S8Gdrn7HnfvAFYD1/WZ5ibgMXePALh7U+8IM5sMvBu4LzklZ46NdS18+P6XGTsql9Ur\nlzKpOD/VJYlICCQS/BVAXdz7+mBYvJnAGDN7zsyqzezDceO+AXwe6DnbQsxspZmtN7P1zc3NCZSV\n3l6pa+FD969lTGGse0ehLyJDJVln9WQDVwBXA/nAb83sJWIbhCZ3rzazZWebgbvfC9wLsfP4k1TX\nsPRqfQu33L+WkoIcHlm5lPIShb6IDJ1Egr8BqIx7PzkYFq8eOOTu7UC7mb0AzAMWAu81s3cBI4Ei\nM/uBu99y4aWnp031rdxy31qK83N45LalVCj0RWSIJdLVsw6YYWbTzCwXuBFY02eaJ4CrzCzbzAqA\nJcA2d/+iu09296nB554Nc+hvbmjl5vteoig/h9UrlzJ5jC5oEpGhN+Aev7t3mdkdwNNAFvCAu28x\ns9uD8fe4+zYzewp4lVhf/n3uvnkwC083sdBfy+iRsT19hb6IpIru1TMEekN/VF42q1cu1a0LRCTp\nzuVePbpyd5BtaWzllvvXUpibpdAXkWFBwT+Itja2cfN9aynIyWL1yjcr9EVkWFDwD5Jt+9q4+b6X\nyM/J4pGVS6kap9AXkeFBwT8IXtsf29PPy45170wZV5jqkkRETlHwJ1nr8U5u/o+15GaNUOiLyLCk\n+/En2ct7D3OovYNVn1jC1FKFvogMP9rjT7Lq2ijZI4wrpoxJdSkiIv1S8CdZTSTKrIpiRuZkpboU\nEZF+KfiTqLO7h1fqWriiSnv7IjJ8KfiTaGtjGye7elg4pSTVpYiInJGCP4lqIlEA9e+LyLCm4E+i\n6too5cUj9VAVERnWFPxJVFMbZYH29kVkmFPwJ8m+1uM0tp7QgV0RGfYU/ElSU9sCqH9fRIY/BX+S\nVNdGycsewWWTilJdiojIWSn4k6QmEmXe5BJys9WkIjK8KaWS4ERnN1saW1mobh4RSQMK/iTY1NBK\nZ7erf19E0oKCPwmqa2MXbi2o0hW7IjL8KfiToKY2ytRxBZSOykt1KSIiA1LwXyB3pyYSVf++iKQN\nBf8Fihw+xsGjHSzUhVsikiYU/BdIN2YTkXSj4L9A1bVRRuVlM3PC6FSXIiKSEAX/BaqubWF+ZQlZ\nIyzVpYiIJETBfwGOnuxi+/42HdgVkbSi4L8Ar9S10OPq3xeR9KLgvwDVtVHMYH6lLtwSkfSRUPCb\n2Qoz225mu8zsrjNMs8zMNprZFjN7PhhWaWa/NLOtwfA7k1l8qtVEoswYP4ri/JxUlyIikrDsgSYw\nsyzgbmA5UA+sM7M17r41bpoS4NvACnePmNn4YFQX8Fl3rzGz0UC1mT0T/9l01dPj1NRGeffcSaku\nRUTknCSyx78Y2OXue9y9A1gNXNdnmpuAx9w9AuDuTcG/+9y9Jnh9BNgGVCSr+FTa3XyUthNdunBL\nRNJOIsFfAdTFva/nd8N7JjDGzJ4zs2oz+3DfmZjZVGABsLa/hZjZSjNbb2brm5ubE6k9pXpvzKYz\nekQk3STr4G42cAXwbuAdwF+b2czekWY2CvgR8Gl3b+tvBu5+r7svcvdFZWVlSSpr8NREopQU5HBR\naWGqSxEROScD9vEDDUBl3PvJwbB49cAhd28H2s3sBWAesMPMcoiF/ip3fywJNQ8L1bVRrqgag5ku\n3BKR9JLIHv86YIaZTTOzXOBGYE2faZ4ArjKzbDMrAJYA2yyWivcD29z9a8ksPJVajnWwu7ld3Twi\nkpYG3ON39y4zuwN4GsgCHnD3LWZ2ezD+HnffZmZPAa8CPcB97r7ZzK4CPgRsMrONwSz/0t2fHJS1\nGSIbIi0AOrArImkpka4egqB+ss+we/q8/yrw1T7DfgVkXF9IdW2UrBHGvMriVJciInLOdOXueaiu\njXL5pCIKchPaboqIDCsK/nPU1d3DK/UtLNTzdUUkTSn4z9Fr+49wrKNbB3ZFJG0p+M+RnrglIulO\nwX+OamqjjB+dR0VJfqpLERE5Lwr+c1QdiXLFFF24JSLpS8F/DpraTlB3+Li6eUQkrSn4z0Fv//4C\nXbglImlMwX8OaiIt5GaNYHZFUapLERE5bwr+c1BdG2XO5GLysrNSXYqIyHlT8CfoZFc3m+pb1b8v\nImlPwZ+gLY1tdHT36IpdEUl7Cv4E1fQ+cUsHdkUkzSn4E1RdG6VybD7ji0amuhQRkQui4E+Au1MT\niWpvX0QygoI/AQ0txznQdlIHdkUkIyj4E1Ct/n0RySAK/gRsiLRQkJvFpRNHp7oUEZELpuBPQHVt\nlHmTS8jOUnOJSPpTkg3gWEcXW/e1qX9fRDKGgn8Ar9a30t3jCn4RyRgK/gH0HthdoCt2RSRDKPgH\nUFMbZXpZISUFuakuRUQkKRT8Z9F74Za6eUQkkyj4z2LvwXaixzp1/r6IZBQF/1n09u9rj19EMomC\n/yxqIlGKRmYzvWxUqksREUkaBf9Z1NS2sKBqDCNGWKpLERFJGgX/GbQe72RH0xF184hIxkko+M1s\nhZltN7NdZnbXGaZZZmYbzWyLmT1/Lp8djjbWteCu/n0RyTzZA01gZlnA3cByoB5YZ2Zr3H1r3DQl\nwLeBFe4eMbPxiX52uKqpjTLCYF6lLtwSkcySyB7/YmCXu+9x9w5gNXBdn2luAh5z9wiAuzedw2eH\npZpIlEsmFjEqb8Bto4hIWkkk+CuAurj39cGweDOBMWb2nJlVm9mHz+GzAJjZSjNbb2brm5ubE6t+\nkHT3OBsiLVwxRXv7IpJ5krU7mw1cAVwN5AO/NbOXzmUG7n4vcC/AokWLPEl1nZedTUc4erJL/fsi\nkpESCf4GoDLu/eRgWLx64JC7twPtZvYCMC8YPtBnhx09cUtEMlkiXT3rgBlmNs3McoEbgTV9pnkC\nuMrMss2sAFgCbEvws8NOdW2U0lG5VI0tSHUpIiJJN+Aev7t3mdkdwNNAFvCAu28xs9uD8fe4+zYz\newp4FegB7nP3zQD9fXaQ1iVpamqjLKwag5ku3BKRzJNQH7+7Pwk82WfYPX3efxX4aiKfHc4OHT3J\n64eOcePiqlSXIiIyKHTlbh81kRZAF26JSOZS8PdRXRslJ8uYU1Gc6lJERAaFgr+PmkiUy8uLGZmT\nlepSREQGhYI/Tmd3D6/UtXCFTuMUkQym4I+ztbGNk1096t8XkYym4I9TEwku3NKtGkQkgyn441TX\nRikvHsmk4vxUlyIiMmgU/HFqaqMsVDePiGQ4BX9gX+txGltPqH9fRDKegj9QUxu7cEs3ZhORTKfg\nD1TXRhmZM4LLy4tSXYqIyKBS8AeqI1HmTi4hJ0tNIiKZTSkHnOjsZmtjq7p5RCQUFPzApoZWOrtd\nB3ZFJBQU/MQ/cUsXbolI5lPwEzt/f1ppIeNG5aW6FBGRQRf64Hd3aiJRFmhvX0RCIvTBHzl8jINH\nO9S/LyKhEfrg770xm4JfRMIi9MFfXRtlVF42M8aPTnUpIiJDQsFf28KCqhKyRliqSxERGRKhDv6j\nJ7vYvr9NF26JSKiEOvhfqWuhx9GtmEUkVEId/NW1UcxgfqVO5RSR8Ah98M8cP5ri/JxUlyIiMmRC\nG/w9Pc6GiJ64JSLhE9rg3918lLYTXbo/j4iETmiDv/fGbLpwS0TCJrTBXxOJMqYgh2mlhakuRURk\nSCUU/Ga2wsy2m9kuM7urn/HLzKzVzDYGP38TN+4zZrbFzDab2SNmNjKZK3C+qmujLKwag5ku3BKR\ncBkw+M3lSjqWAAAI+ElEQVQsC7gbeCdwOfBBM7u8n0lfdPf5wc/fBZ+tAD4FLHL32UAWcGPSqj9P\nLcc62N3crgO7IhJKiezxLwZ2ufsed+8AVgPXncMysoF8M8sGCoDGcy8zuTZEWgD174tIOCUS/BVA\nXdz7+mBYX1ea2atm9j9mNgvA3RuAfwUiwD6g1d1/1t9CzGylma03s/XNzc3ntBLnqro2StYIY+7k\n4kFdjojIcJSsg7s1QJW7zwX+HXgcwMzGEPt2MA0oBwrN7Jb+ZuDu97r7IndfVFZWlqSy+lddG+Xy\nSUUU5GYP6nJERIajRIK/AaiMez85GHaKu7e5+9Hg9ZNAjpmVAtcAe9292d07gceAK5NS+Xnq6u7h\nlfoWdfOISGglEvzrgBlmNs3McokdnF0TP4GZTbTg9BgzWxzM9xCxLp6lZlYQjL8a2JbMFThXr+0/\nwrGObh3YFZHQGrCvw927zOwO4GliZ+U84O5bzOz2YPw9wA3An5hZF3AcuNHdHVhrZo8S6wrqAjYA\n9w7OqiSm94lbumJXRMIqoU7uoPvmyT7D7ol7/S3gW2f47JeAL11AjUlVXRtlQlEeFSX5qS5FRCQl\nQnflbk0kyhVTdOGWiIRXqIK/qe0EdYeP64lbIhJqoQr+U/37OrArIiEWsuBvITd7BLPKi1JdiohI\nyoQq+Ktro8ypKCYvOyvVpYiIpExogv9kVzeb6lt14ZaIhF5ogn9LYxsd3T06sCsioRea4K+p7T2w\nqwu3RCTcQhP81bVRKsfmM370sHgOjIhIyoQi+N09duGWunlERMIR/A0txznQdlIHdkVECEnwVwf9\n+wu0xy8iEo7gr6mNUpCbxaUTR6e6FBGRlAtH8EdamF9ZQnZWKFZXROSsMj4Jj3V0sXVfm87fFxEJ\nZHzwv1LXSneP68CuiEgg44O/946cC/TELRERIAzBXxvl4vGjKCnITXUpIiLDQkYHf++FW3q+rojI\nGzI6+PcebCd6rFP9+yIicTI6+Hsv3FLwi4i8IaODvyYSpWhkNheVjkp1KSIiw0ZmB39tCwunjGHE\nCEt1KSIiw0bGBn/r8U52NB3RHTlFRPrI2ODfWNeCOyxU/76IyGkyNvhraqOMMJhXqVM5RUTiZW7w\nR6JcOrGIUXnZqS5FRGRYycjg7+5xNkRadBqniEg/MjL4dxw4wtGTXXqwuohIPxIKfjNbYWbbzWyX\nmd3Vz/hlZtZqZhuDn7+JG1diZo+a2Wtmts3M3pzMFehP743ZrqgaO9iLEhFJOwN2gJtZFnA3sByo\nB9aZ2Rp339pn0hfd/dp+ZvFN4Cl3v8HMcoGCCy16INW1UUpH5VE5Nn+wFyUiknYS2eNfDOxy9z3u\n3gGsBq5LZOZmVgy8DbgfwN073L3lfItNVE1t7MZsZrpwS0Skr0SCvwKoi3tfHwzr60oze9XM/sfM\nZgXDpgHNwHfNbIOZ3Wdmhf0txMxWmtl6M1vf3Nx8LutwmkNHT/L6oWM6sCsicgbJOrhbA1S5+1zg\n34HHg+HZwELgO+6+AGgHfucYAYC73+vui9x9UVlZ2fkXEol9oVDwi4j0L5HgbwAq495PDoad4u5t\n7n40eP0kkGNmpcS+HdS7+9pg0keJbQgGTXVtlJwsY3ZF8WAuRkQkbSUS/OuAGWY2LTg4eyOwJn4C\nM5toQYe6mS0O5nvI3fcDdWZ2STDp1UDfg8JJVROJMqu8mJE5WYO5GBGRtDXgWT3u3mVmdwBPA1nA\nA+6+xcxuD8bfA9wA/ImZdQHHgRvd3YNZ/BmwKtho7AE+OgjrAUBndw+v1LVwy9Ipg7UIEZG0l9D9\nDILumyf7DLsn7vW3gG+d4bMbgUUXUGPCtja2cbKrR/37IiJnkVFX7vZeuLVQt2IWETmjjAr+6too\nFSX5TCwemepSRESGrYwK/praqO6/LyIygIy5Z/HJrm7ecnEpV80oTXUpIiLDWsYEf152Fl/9w3mp\nLkNEZNjLqK4eEREZmIJfRCRkFPwiIiGj4BcRCRkFv4hIyCj4RURCRsEvIhIyCn4RkZCxN+6ePHyY\nWTNQe5ZJSoGDQ1ROOlB7vEFtcTq1x+kyuT2muHtCjy8clsE/EDNb7+5DcqvndKD2eIPa4nRqj9Op\nPWLU1SMiEjIKfhGRkEnX4L831QUMM2qPN6gtTqf2OJ3agzTt4xcRkfOXrnv8IiJynhT8IiIhk1bB\nb2YrzGy7me0ys7tSXc9QM7MHzKzJzDbHDRtrZs+Y2c7g39A8e9LMKs3sl2a21cy2mNmdwfDQtYmZ\njTSzl83slaAtvhwMD11bxDOzLDPbYGY/Cd6Huj16pU3wm1kWcDfwTuBy4INmdnlqqxpyDwIr+gy7\nC/iFu88AfhG8D4su4LPufjmwFPhk8DcRxjY5Cbzd3ecB84EVZraUcLZFvDuBbXHvw94eQBoFP7AY\n2OXue9y9A1gNXJfimoaUu78AHO4z+DrgoeD1Q8D1Q1pUCrn7PnevCV4fIfYfvIIQtonHHA3e5gQ/\nTgjbopeZTQbeDdwXNzi07REvnYK/AqiLe18fDAu7Ce6+L3i9H5iQymJSxcymAguAtYS0TYJujY1A\nE/CMu4e2LQLfAD4P9MQNC3N7nJJOwS8D8Ni5uaE7P9fMRgE/Aj7t7m3x48LUJu7e7e7zgcnAYjOb\n3Wd8aNrCzK4Fmty9+kzThKk9+kqn4G8AKuPeTw6Ghd0BM5sEEPzblOJ6hpSZ5RAL/VXu/lgwONRt\n4u4twC+JHQ8Ka1u8BXivmb1OrFv47Wb2A8LbHqdJp+BfB8wws2lmlgvcCKxJcU3DwRrg1uD1rcAT\nKaxlSJmZAfcD29z9a3GjQtcmZlZmZiXB63xgOfAaIWwLAHf/ortPdvepxLLiWXe/hZC2R19pdeWu\nmb2LWL9dFvCAu38lxSUNKTN7BFhG7NayB4AvAY8DPwSqiN3K+gPu3vcAcEYys6uAF4FNvNGP+5fE\n+vlD1SZmNpfYwcosYjt0P3T3vzOzcYSsLfoys2XA59z9WrVHTFoFv4iIXLh06uoREZEkUPCLiISM\ngl9EJGQU/CIiIaPgFxEJGQW/iEjIKPhFRELm/wNGEXdXRuj19AAAAABJRU5ErkJggg==\n",
"text/plain": [
"<matplotlib.figure.Figure at 0x1ea04dba198>"
]
},
"metadata": {},
"output_type": "display_data"
}
],
"source": [
"plt.plot(list_estimators, et_scoring)\n",
"plt.title('Accuracy VS trees number');"
]
},
{
"cell_type": "code",
"execution_count": 17,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"ExtraTreesClassifier(bootstrap=False, class_weight='balanced',\n",
" criterion='gini', max_depth=None, max_features='auto',\n",
" max_leaf_nodes=None, min_impurity_decrease=0.0,\n",
" min_impurity_split=None, min_samples_leaf=1,\n",
" min_samples_split=2, min_weight_fraction_leaf=0.0,\n",
" n_estimators=12, n_jobs=-1, oob_score=False, random_state=4536,\n",
" verbose=0, warm_start=False)"
]
},
"execution_count": 17,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"classifier = ExtraTreesClassifier(random_state = rnd_state, n_jobs = -1, \n",
" class_weight='balanced', n_estimators=12)\n",
"classifier.fit(predictors_train, target_train)"
]
},
{
"cell_type": "code",
"execution_count": 18,
"metadata": {},
"outputs": [],
"source": [
"prediction = classifier.predict(predictors_test)"
]
},
{
"cell_type": "code",
"execution_count": 19,
"metadata": {},
"outputs": [
{
"name": "stdout",
"output_type": "stream",
"text": [
"Confusion matrix:\n",
" Predicted 3 4 5 6 7 8 All\n",
"Actual \n",
"3 0 1 2 0 0 0 3\n",
"4 0 0 9 7 0 0 16\n",
"5 2 2 168 39 2 0 213\n",
"6 0 0 49 130 11 1 191\n",
"7 0 0 2 27 24 0 53\n",
"8 0 0 0 3 1 0 4\n",
"All 2 3 230 206 38 1 480\n",
"\n",
"Accuracy: 0.6708333333333333\n"
]
}
],
"source": [
"print('Confusion matrix:\\n', pd.crosstab(target_test, prediction, colnames=['Predicted'], \n",
" rownames=['Actual'], margins=True))\n",
"print('\\nAccuracy: ', accuracy_score(target_test, prediction))"
]
},
{
"cell_type": "code",
"execution_count": 20,
"metadata": {},
"outputs": [
{
"data": {
"text/plain": [
"alcohol 0.157267\n",
"volatile acidity 0.132768\n",
"sulphates 0.100874\n",
"citric acid 0.095077\n",
"density 0.082334\n",
"chlorides 0.079283\n",
"total sulfur dioxide 0.076803\n",
"pH 0.074638\n",
"fixed acidity 0.069826\n",
"residual sugar 0.066551\n",
"free sulfur dioxide 0.064579\n",
"dtype: float64"
]
},
"execution_count": 20,
"metadata": {},
"output_type": "execute_result"
}
],
"source": [
"feature_importance = pd.Series(classifier.feature_importances_, \n",
" index=data.columns.values[:11]).sort_values(ascending=False)\n",
"feature_importance"
]
}
],
"metadata": {
"kernelspec": {
"display_name": "Python 3",
"language": "python",
"name": "python3"
},
"language_info": {
"codemirror_mode": {
"name": "ipython",
"version": 3
},
"file_extension": ".py",
"mimetype": "text/x-python",
"name": "python",
"nbconvert_exporter": "python",
"pygments_lexer": "ipython3",
"version": "3.6.3"
},
"widgets": {
"state": {},
"version": "1.1.2"
}
},
"nbformat": 4,
"nbformat_minor": 1
}
2. result
Task
The second assignment deals with Random Forests. Random forests are predictive models that allow for a data driven exploration of many explanatory variables in predicting a response or target variable. Random forests provide importance scores for each explanatory variable and also allow you to evaluate any increases in correct classification with the growing of smaller and larger number of trees.
Run a Random Forest.
You will need to perform a random forest analysis to evaluate the importance of a series of explanatory variables in predicting a binary, categorical response variable.
Data
The dataset is related to red variants of the Portuguese "Vinho Verde" wine. Due to privacy and logistic issues, only physicochemical (inputs) and sensory (the output) variables are available (e.g. there is no data about grape types, wine brand, wine selling price, etc.).
The classes are ordered and not balanced (e.g. there are munch more normal wines than excellent or poor ones). Outlier detection algorithms could be used to detect the few excellent or poor wines. Also, we are not sure if all input variables are relevant. So it could be interesting to test feature selection methods.
Dataset can be found at UCI Machine Learning Repository
Attribute Information (For more information, read [Cortez et al., 2009]): Input variables (based on physicochemical tests):
- 1 - fixed acidity
- 2 - volatile acidity
- 3 - citric acid
- 4 - residual sugar
- 5 - chlorides
- 6 - free sulfur dioxide
- 7 - total sulfur dioxide
- 8 - density
- 9 - pH
- 10 - sulphates
- 11 - alcohol
Output variable (based on sensory data):
- 12 - quality (score between 0 and 10)
Results
Random forest and ExtraTrees classifier were deployed to evaluate the importance of a series of explanatory variables in predicting a categorical response variable - red wine quality (score between 0 and 10). The following explanatory variables were included: fixed acidity, volatile acidity, citric acid, residual sugar, chlorides, free sulfur dioxide, total sulfur dioxide, density, pH, sulphates and alcohol.
The explanatory variables with the highest importance score (evaluated by both classifiers) are alcohol, volatile acidity, sulphates. The accuracy of the Random forest and ExtraTrees clasifier is about 67%, which is quite good for highly unbalanced and hardly distinguished from each other classes. The subsequent growing of multiple trees rather than a single tree, adding a lot to the overall score of the model. For Random forest the number of estimators is 20, while for ExtraTrees classifier - 12, because the second classifier grows up much faster.
Code
import pandas as pdimport numpy as npimport matplotlib.pylab as pltfrom sklearn.model_selection import train_test_split, cross_val_scorefrom sklearn.ensemble import RandomForestClassifier, ExtraTreesClassifierfrom sklearn.manifold import MDSfrom sklearn.metrics.pairwise import pairwise_distancesfrom sklearn.metrics import accuracy_scoreimport seaborn as sns%matplotlib inlinernd_state = 4536
data = pd.read_csv('Data\winequality-red.csv', sep=';')data.info()<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1599 entries, 0 to 1598
Data columns (total 12 columns):
fixed acidity 1599 non-null float64
volatile acidity 1599 non-null float64
citric acid 1599 non-null float64
residual sugar 1599 non-null float64
chlorides 1599 non-null float64
free sulfur dioxide 1599 non-null float64
total sulfur dioxide 1599 non-null float64
density 1599 non-null float64
pH 1599 non-null float64
sulphates 1599 non-null float64
alcohol 1599 non-null float64
quality 1599 non-null int64
dtypes: float64(11), int64(1)
memory usage: 150.0 KB
data.head()| 7.4 | 0.70 | 0.00 | 1.9 | 0.076 | 11.0 | 34.0 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 |
| 7.8 | 0.88 | 0.00 | 2.6 | 0.098 | 25.0 | 67.0 | 0.9968 | 3.20 | 0.68 | 9.8 | 5 |
| 7.8 | 0.76 | 0.04 | 2.3 | 0.092 | 15.0 | 54.0 | 0.9970 | 3.26 | 0.65 | 9.8 | 5 |
| 11.2 | 0.28 | 0.56 | 1.9 | 0.075 | 17.0 | 60.0 | 0.9980 | 3.16 | 0.58 | 9.8 | 6 |
| 7.4 | 0.70 | 0.00 | 1.9 | 0.076 | 11.0 | 34.0 | 0.9978 | 3.51 | 0.56 | 9.4 | 5 |
data.describe()| 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 | 1599.000000 |
| 8.319637 | 0.527821 | 0.270976 | 2.538806 | 0.087467 | 15.874922 | 46.467792 | 0.996747 | 3.311113 | 0.658149 | 10.422983 | 5.636023 |
| 1.741096 | 0.179060 | 0.194801 | 1.409928 | 0.047065 | 10.460157 | 32.895324 | 0.001887 | 0.154386 | 0.169507 | 1.065668 | 0.807569 |
| 4.600000 | 0.120000 | 0.000000 | 0.900000 | 0.012000 | 1.000000 | 6.000000 | 0.990070 | 2.740000 | 0.330000 | 8.400000 | 3.000000 |
| 7.100000 | 0.390000 | 0.090000 | 1.900000 | 0.070000 | 7.000000 | 22.000000 | 0.995600 | 3.210000 | 0.550000 | 9.500000 | 5.000000 |
| 7.900000 | 0.520000 | 0.260000 | 2.200000 | 0.079000 | 14.000000 | 38.000000 | 0.996750 | 3.310000 | 0.620000 | 10.200000 | 6.000000 |
| 9.200000 | 0.640000 | 0.420000 | 2.600000 | 0.090000 | 21.000000 | 62.000000 | 0.997835 | 3.400000 | 0.730000 | 11.100000 | 6.000000 |
| 15.900000 | 1.580000 | 1.000000 | 15.500000 | 0.611000 | 72.000000 | 289.000000 | 1.003690 | 4.010000 | 2.000000 | 14.900000 | 8.000000 |
Plots
For visualization purposes, the number of dimensions was reduced to two by applying MDS method with cosine distance. The plot illustrates that our classes are not clearly divided into parts.
model = MDS(random_state=rnd_state, n_components=2, dissimilarity='precomputed')%time representation = model.fit_transform(pairwise_distances(data.iloc[:, :11], metric='cosine'))Wall time: 38.7 s
colors = ["#9b59b6", "#3498db", "#95a5a6", "#e74c3c", "#34495e", "#2ecc71"]plt.figure(figsize=(12, 4))plt.subplot(121)plt.scatter(representation[:, 0], representation[:, 1], c=colors)plt.subplot(122)sns.countplot(x='quality', data=data, palette=sns.color_palette(colors));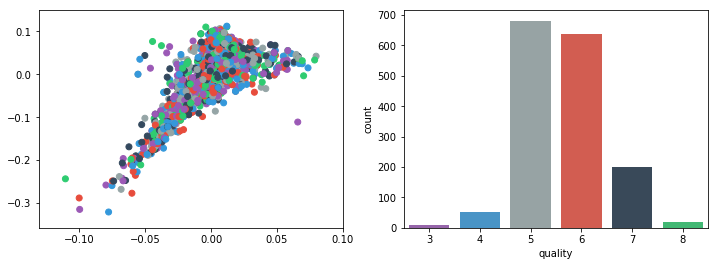
Moreover, our classes are highly unbalanced, so in our classifier we should add parameter class_weight='balanced'.
predictors = data.iloc[:, :11]target = data.quality
(predictors_train, predictors_test, target_train, target_test) = train_test_split(predictors, target, test_size = .3, random_state = rnd_state)RandomForest classifier
list_estimators = list(range(1, 50, 5))rf_scoring = []for n_estimators in list_estimators: classifier = RandomForestClassifier(random_state = rnd_state, n_jobs = -1, class_weight='balanced', n_estimators=n_estimators) score = cross_val_score(classifier, predictors_train, target_train, cv=5, n_jobs=-1, scoring = 'accuracy') rf_scoring.append(score.mean())
plt.plot(list_estimators, rf_scoring)plt.title('Accuracy VS trees number');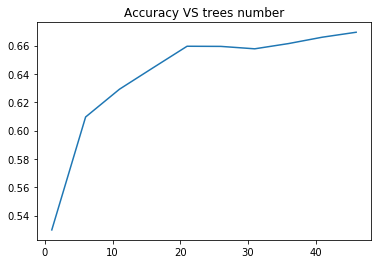
classifier = RandomForestClassifier(random_state = rnd_state, n_jobs = -1, class_weight='balanced', n_estimators=20)classifier.fit(predictors_train, target_train)RandomForestClassifier(bootstrap=True, class_weight='balanced',
criterion='gini', max_depth=None, max_features='auto',
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=20, n_jobs=-1, oob_score=False, random_state=4536,
verbose=0, warm_start=False)
prediction = classifier.predict(predictors_test)
print('Confusion matrix:\n', pd.crosstab(target_test, prediction, colnames=['Predicted'], rownames=['Actual'], margins=True))print('\nAccuracy: ', accuracy_score(target_test, prediction))Confusion matrix:
Predicted 3 4 5 6 7 All
Actual
3 0 0 3 0 0 3
4 0 1 9 6 0 16
5 2 1 166 41 3 213
6 0 0 46 131 14 191
7 0 0 5 25 23 53
8 0 0 0 3 1 4
All 2 2 229 206 41 480
Accuracy: 0.66875
feature_importance = pd.Series(classifier.feature_importances_, index=data.columns.values[:11]).sort_values(ascending=False)feature_importancevolatile acidity 0.133023
alcohol 0.130114
sulphates 0.129498
citric acid 0.106427
total sulfur dioxide 0.094647
chlorides 0.086298
density 0.079843
pH 0.066566
residual sugar 0.061344
fixed acidity 0.058251
free sulfur dioxide 0.053990
dtype: float64
et_scoring = []for n_estimators in list_estimators: classifier = ExtraTreesClassifier(random_state = rnd_state, n_jobs = -1, class_weight='balanced', n_estimators=n_estimators) score = cross_val_score(classifier, predictors_train, target_train, cv=5, n_jobs=-1, scoring = 'accuracy') et_scoring.append(score.mean())
plt.plot(list_estimators, et_scoring)plt.title('Accuracy VS trees number');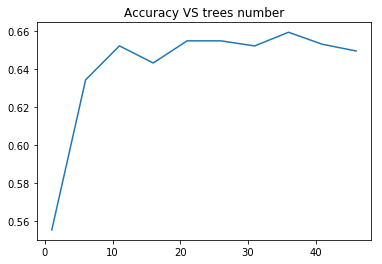
classifier = ExtraTreesClassifier(random_state = rnd_state, n_jobs = -1, class_weight='balanced', n_estimators=12)classifier.fit(predictors_train, target_train)ExtraTreesClassifier(bootstrap=False, class_weight='balanced',
criterion='gini', max_depth=None, max_features='auto',
max_leaf_nodes=None, min_impurity_decrease=0.0,
min_impurity_split=None, min_samples_leaf=1,
min_samples_split=2, min_weight_fraction_leaf=0.0,
n_estimators=12, n_jobs=-1, oob_score=False, random_state=4536,
verbose=0, warm_start=False)
prediction = classifier.predict(predictors_test)
print('Confusion matrix:\n', pd.crosstab(target_test, prediction, colnames=['Predicted'], rownames=['Actual'], margins=True))print('\nAccuracy: ', accuracy_score(target_test, prediction))Confusion matrix:
Predicted 3 4 5 6 7 8 All
Actual
3 0 1 2 0 0 0 3
4 0 0 9 7 0 0 16
5 2 2 168 39 2 0 213
6 0 0 49 130 11 1 191
7 0 0 2 27 24 0 53
8 0 0 0 3 1 0 4
All 2 3 230 206 38 1 480
Accuracy: 0.6708333333333333
feature_importance = pd.Series(classifier.feature_importances_, index=data.columns.values[:11]).sort_values(ascending=False)feature_importancealcohol 0.157267
volatile acidity 0.132768
sulphates 0.100874
citric acid 0.095077
density 0.082334
chlorides 0.079283
total sulfur dioxide 0.076803
pH 0.074638
fixed acidity 0.069826
residual sugar 0.066551
free sulfur dioxide 0.064579
dtype: float64
3. comment
The second assignment deals with Random Forests. Random forests are predictive models that allow for a data driven exploration of many explanatory variables in predicting a response or target variable. Random forests provide importance scores for each explanatory variable and also allow you to evaluate any increases in correct classification with the growing of smaller and larger number of trees.
Run a Random Forest.
You will need to perform a random forest analysis to evaluate the importance of a series of explanatory variables in predicting a binary, categorical response variable.